独立ではない2つの確率変数の積の期待値を求めました。

コード
数式を使った計算
# 2021 Q1(4) 2024.8.20
import sympy as sp
# シンボリック変数の定義
x, y = sp.symbols('x y')
# h(x) の導出
h_x = sp.integrate(sp.exp(-x), (x, 0, x))
# XY の期待値の計算
# h(x) = 1 - exp(-x) を使って E[X * h(X)] を計算する
integral_part1 = sp.integrate(x * h_x * sp.exp(-x), (x, 0, sp.oo))
E_XY_simplified = sp.simplify(integral_part1)
# 結果の表示
display(sp.Eq(sp.Symbol('h(x)'), h_x))
display(sp.Eq(sp.Symbol('E[XY]'), E_XY_simplified))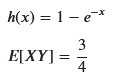
指数分布に従う乱数Xを生成し、Y=h(X)Yが一様分布に従うか確認
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# ヒストグラムのプロット
plt.figure(figsize=(8, 5))
plt.hist(Y_samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションされた Y=h(X)')
plt.xlabel('y')
plt.ylabel('密度')
plt.title('Y = h(X) の分布 (シミュレーション結果)')
plt.legend()
plt.grid(True)
plt.show()
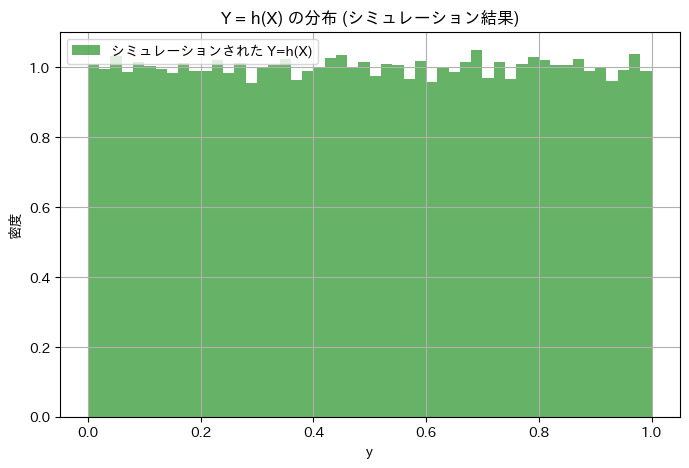
シミュレーションによるE[XY]の計算
import numpy as np
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# XY の期待値を計算
XY_samples = X_samples * Y_samples
E_XY_simulation = np.mean(XY_samples)
# 結果の表示
print(f"シミュレーションによる E[XY] = {E_XY_simulation}")
print(f"理論値 E[XY] = 3/4 = {3/4}")シミュレーションによる E[XY] = 0.7473462073557277
理論値 E[XY] = 3/4 = 0.75