指数分布と一様分布の期待値と、それらが独立な場合の積の期待値を求めました。
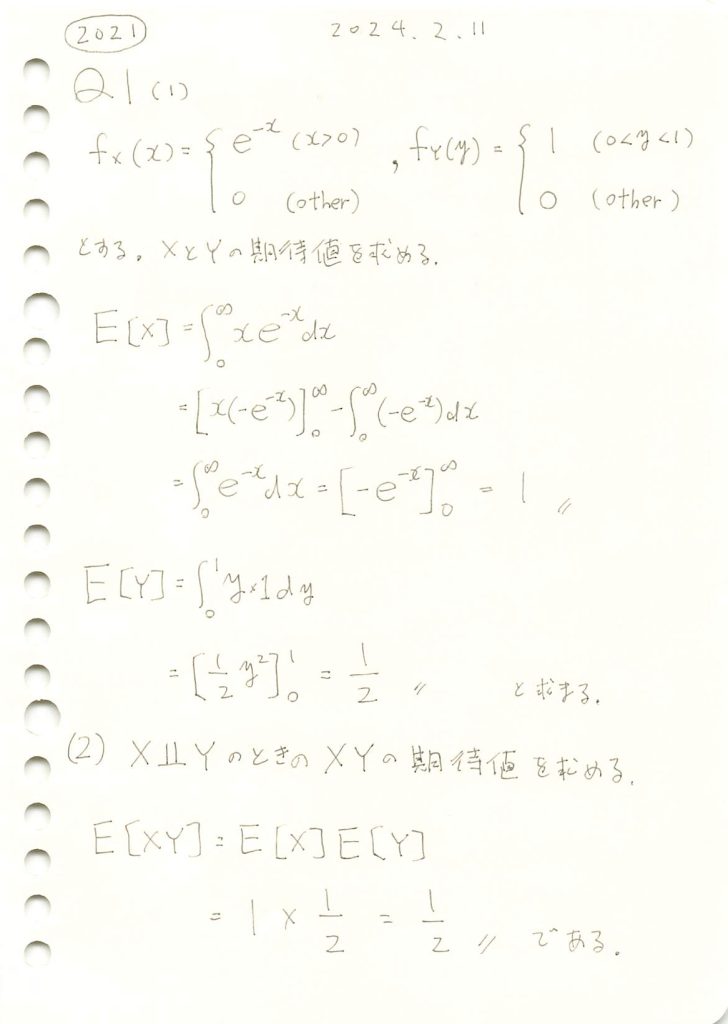
コード
数式を使った計算
# 2021 Q1(1)(2) 2024.8.18
import numpy as np
from scipy.integrate import quad
# Xの期待値の計算
def fx(x):
return x * np.exp(-x)
E_X, _ = quad(fx, 0, np.inf)
# Yの期待値の計算
def fy(y):
return y
E_Y, _ = quad(fy, 0, 1)
# XYの期待値の計算(独立の場合)
E_XY = E_X * E_Y
print(f"E[X] = {E_X}")
print(f"E[Y] = {E_Y}")
print(f"E[XY] (独立の場合) = {E_XY}")
E[X] = 0.9999999999999998
E[Y] = 0.5
E[XY] (独立の場合) = 0.4999999999999999シミュレーションによる計算
# 2021 Q1(1)(2) 2024.8.18
import numpy as np
# シミュレーションの設定
num_samples = 1000000 # サンプル数
# Xの乱数生成(指数分布)
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# Yの乱数生成(一様分布)
Y_samples = np.random.uniform(0, 1, size=num_samples)
# (1) XとYの期待値の計算
E_X_simulation = np.mean(X_samples)
E_Y_simulation = np.mean(Y_samples)
# (2) XYの期待値の計算(独立な場合)
E_XY_simulation = np.mean(X_samples * Y_samples)
print(f"E[X] = {E_X_simulation}")
print(f"E[Y] = {E_Y_simulation}")
print(f"E[XY] = {E_XY_simulation}")
E[X] = 1.0001064255963075
E[Y] = 0.4998284579940602
E[XY] = 0.4998038319582688