一様分布の最大値を条件とする条件付き同時確率密度関数の問題をやりました。

コード
一様分布の最大値を条件とする条件付き同時確率密度関数が
![]()
となるかをシミュレーションで確認しました。Yを1~10に変化させて、Y以下の乱数を発生させてカーネル密度推定で同時確率密度を計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde
# パラメータ設定
n = 15 # サンプルサイズ
num_simulations = 10000 # シミュレーション回数
Y_values = np.arange(1, 11, 1) # Y を 1 から 10 に変化させる
# シミュレーション結果を格納するリスト
simulated_f_values = [] # シミュレーションによる f の値
theoretical_f_values = [] # 理論値 f(x_1, ..., x_{n-1} | Y=y)
# シミュレーション開始
for Y in Y_values:
f_sim_sum = 0 # f(x_1, ..., x_{n-1} | Y=y) の合計
for _ in range(num_simulations):
# Y より小さい範囲で n-1 個のサンプルを生成し、観測された最大値 Y を追加
samples = np.random.uniform(0, Y, n-1)
samples = np.append(samples, Y) # 観測値としての Y を追加
# カーネル密度推定を実行
kde = gaussian_kde(samples) # サンプルに基づいてKDEを実行
# samples から Y (最後の要素) を除いた部分で密度を計算
f_sim = np.prod(kde.evaluate(samples[:-1])) # サンプルごとの確率密度を掛け合わせる
# f(y) = 1 として扱う(条件付き分布)
f_sim_sum += f_sim
# シミュレーション結果の平均をリストに追加
simulated_f_values.append(f_sim_sum / num_simulations)
# 理論値 1 / Y^(n-1) を計算
theoretical_f_values.append(1 / Y**(n-1))
# グラフ描画
plt.plot(Y_values, simulated_f_values, 'bo-', label='シミュレーション結果')
plt.plot(Y_values, theoretical_f_values, 'r--', label='理論値 1/Y^(n-1)')
# 縦軸を対数スケールに変更
plt.yscale('log')
# グラフ設定
plt.title(f'f(x1, ..., xn-1 | Y=y) のシミュレーション結果と理論値 (n={n})')
plt.xlabel('Y の値')
plt.ylabel('f(x1, ..., xn-1 | Y=y)')
plt.legend()
plt.grid(True)
plt.show()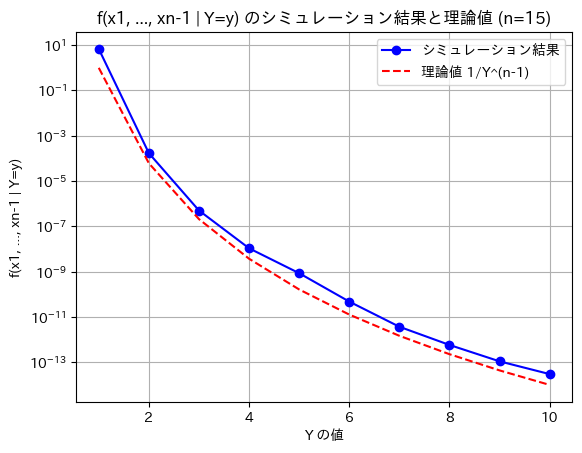
概ね理論値と一致しました。カーネル密度推定の誤差により、シミュレーションの値は理論値より少し大きくなっていると思われます。