一様分布の最大値をとる確率変数の確率密度関数を求めました。
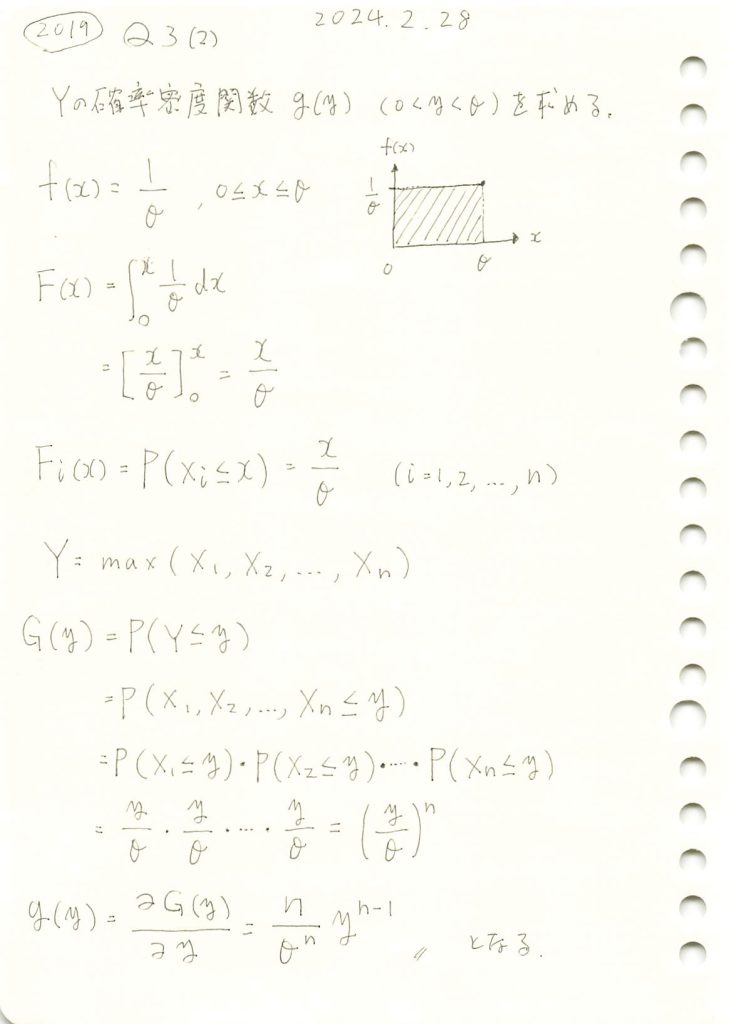
コード
数式を使って確率密度関数g(y)を求めます。
# 2019 Q3(2) 2024.9.18
import sympy as sp
# 変数を定義
y, theta, n = sp.symbols('y theta n')
# 累積分布関数 F_Y(y) を定義
F_Y = (y / theta)**n # F_Y(y) = (y / θ)^n
# 確率密度関数 g(y) を F_Y(y) の y に関する微分として計算
g_y = sp.diff(F_Y, y)
# 簡略化
g_y_simplified = sp.simplify(g_y)
# 結果を表示
display(g_y_simplified)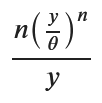
形は少し違いますが、正しいです。
得られた確率密度関数g(y)と数値シミュレーションによる分布と比較します。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
n = 10 # サンプルサイズ(n個の一様分布からのサンプル)
theta = 10 # 一様分布の上限
num_simulations = 10000 # シミュレーション回数
# 最大値 Y のリスト
Y_values = []
# シミュレーション
for _ in range(num_simulations):
samples = np.random.uniform(0, theta, n) # (0, θ)の範囲からn個のサンプルを生成
Y = np.max(samples) # 最大値を計算
Y_values.append(Y)
# ヒストグラムを描画
plt.hist(Y_values, bins=30, density=True, alpha=0.7, color='blue', edgecolor='black', label='シミュレーション結果')
# 理論上の確率密度関数を描画
y = np.linspace(0, theta, 1000)
g_y = (n / theta**n) * y**(n-1)
plt.plot(y, g_y, color='red', label='理論的な分布')
# グラフの設定
plt.title(f'最大値 Y の分布と理論的分布 (n={n}, θ={theta})')
plt.xlabel('最大値 Y')
plt.ylabel('確率密度')
plt.legend()
plt.show()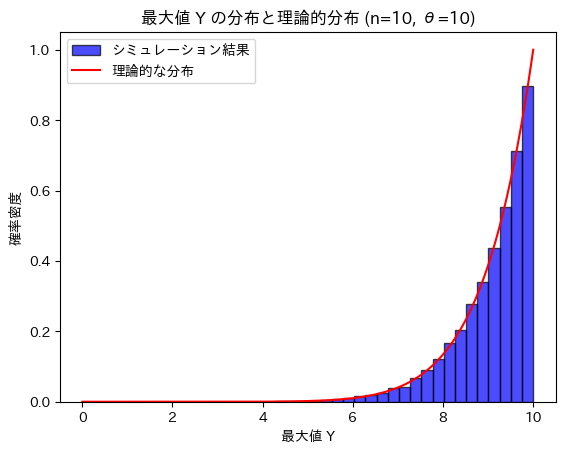
確率密度関数g(y)と数値シミュレーションによる分布は一致することが確認できました。