一様分布に於いて最大値が十分統計量であることを示しました。

コード
一様分布の最大値Yを元に、不偏推定量![]() を計算します。
を計算します。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータ
n = 10 # サンプルサイズ
theta_true = 10 # 真のθ
num_simulations = 1000 # シミュレーション回数
# θの推定値を格納するリスト
theta_estimates = []
# シミュレーション開始
for _ in range(num_simulations):
# (0, theta_true) の一様分布からn個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# 最大値 Y = max(X_1, ..., X_n)
Y = np.max(samples)
# Y から θ を推定 (最大値を使って推定)
theta_hat = Y * (n / (n - 1)) # 推定式: Y * n / (n-1)
# 推定されたθをリストに保存
theta_estimates.append(theta_hat)
# θの推定値の平均を計算
theta_mean = np.mean(theta_estimates)
# 推定結果をヒストグラムで表示
plt.hist(theta_estimates, bins=30, alpha=0.7, color='blue', edgecolor='black', label='推定されたθ')
plt.axvline(x=theta_true, color='red', linestyle='--', label=f'真のθ = {theta_true}')
plt.axvline(x=theta_mean, color='green', linestyle='--', label=f'推定されたθの平均 = {theta_mean:.2f}')
plt.title(f'Y (最大値) に基づく θ の推定値のヒストグラム ({n} サンプル)')
plt.xlabel('推定された θ')
plt.ylabel('頻度')
plt.legend()
plt.show()
# 推定結果をテキストで表示
print(f'真のθ: {theta_true}')
print(f'推定されたθの平均: {theta_mean:.2f}')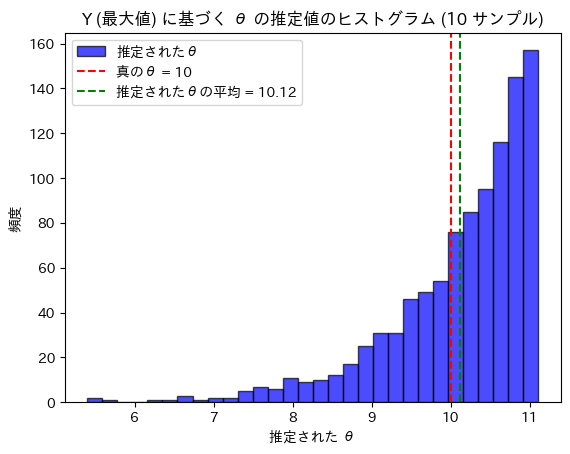
真のθ: 10
推定されたθの平均: 10.12推定されたθは真のθに近い値を取りました。最大値Yだけを用いてθが正確に推定できたので、Yはθに関する十分統計量であることが確認できました。