独立な指数分布に従う2変数の和の期待値を求めました。
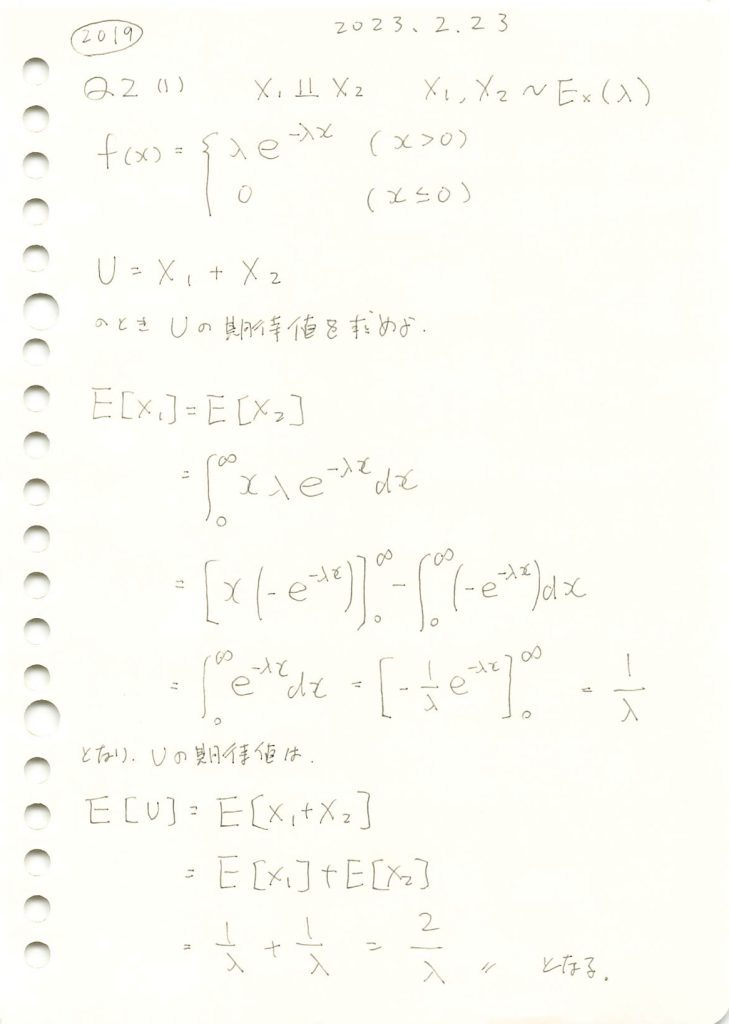
コード
数式を使ってUの期待値を求めます
import sympy as sp
# 変数の定義
x = sp.Symbol('x', positive=True)
lambda_value = sp.Symbol('lambda', positive=True)
# 指数分布の確率密度関数 (PDF)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 期待値の式を計算 (積分)
E_X1 = sp.integrate(x * f_x, (x, 0, sp.oo))
# 期待値
E_X1_simplified = sp.simplify(E_X1)
# X1 + X2 の場合 (独立性より)
E_U = 2 * E_X1_simplified
# 結果の表示
display(E_U)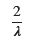
手計算と一致します
次にUに従う乱数を生成し分布を確認します。また形状パラメータ2のガンマ分布と重ねて描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 例としてλ=2
num_samples = 1000 # サンプルの数
# 指数分布に従う乱数の生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 理論的な期待値
expected_value = 2 / lambda_value
# シミュレーション結果のヒストグラムのプロット (確率密度にスケール)
plt.hist(U, bins=30, density=True, alpha=0.7, label='シミュレーション結果')
# ガンマ分布 (形状パラメータ k=2, スケールパラメータ θ=1/λ) の確率密度関数 (PDF) を計算
k = 2 # 形状パラメータ (k = 2)
theta = 1 / lambda_value # スケールパラメータ (θ = 1/λ)
# ガンマ分布に基づくx軸の範囲
x = np.linspace(0, max(U), 1000)
# ガンマ分布の確率密度関数 (PDF) を計算
gamma_pdf = gamma.pdf(x, a=k, scale=theta)
# ガンマ分布の折れ線グラフをプロット
plt.plot(x, gamma_pdf, 'r-', label=f'ガンマ分布 (k={k}, θ={theta:.2f})')
# グラフの装飾
plt.axvline(expected_value, color='g', linestyle='--', label=f'理論値 = {expected_value:.2f}')
plt.xlabel('U = X1 + X2')
plt.ylabel('確率密度')
plt.title('Uの分布とガンマ分布の比較')
plt.legend()
plt.show()
# 実際のサンプル平均値と理論的期待値の比較
print(f'理論的な期待値: {expected_value}')
print(f'シミュレーションからの平均値: {np.mean(U)}')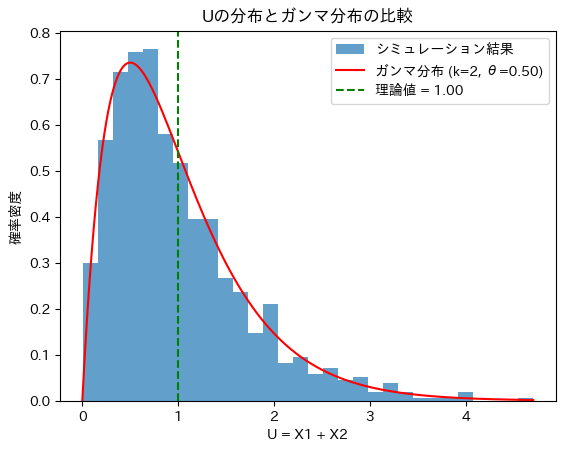
理論的な期待値: 1.0
シミュレーションからの平均値: 0.9902440726761544Uの分布と形状パラメータ2のガンマ分布は重なりました。Uはガンマ分布に従うことが分かります。