一様分布の3つの順序統計量のうち真ん中の確率密度関数と確率の計算をしました。
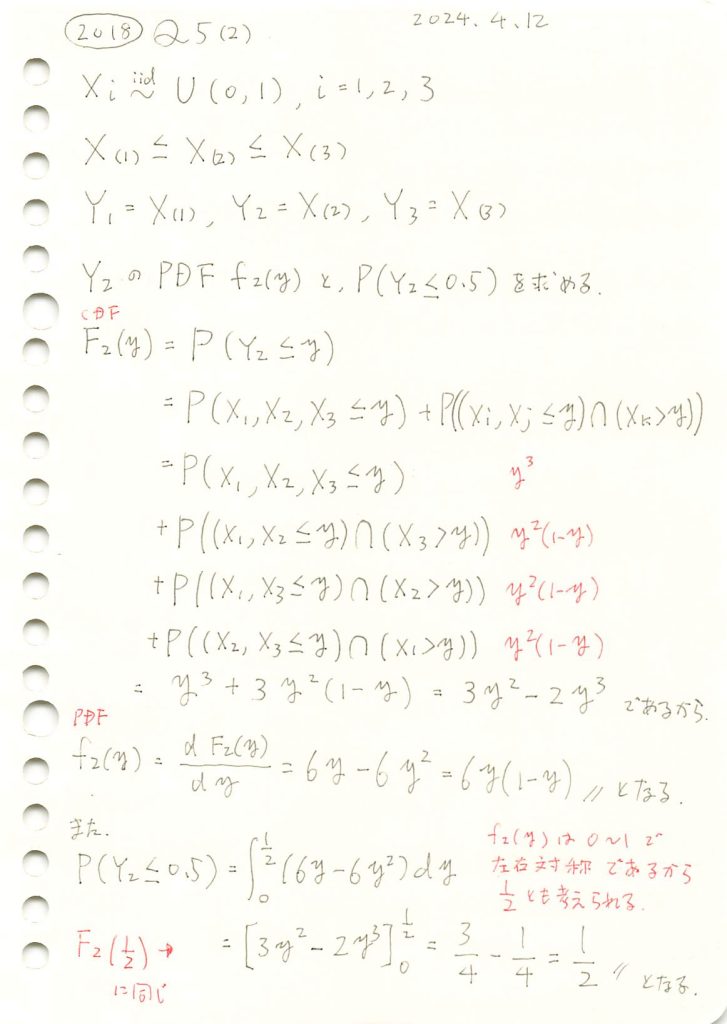
コード
シミュレーションにより順序統計量Y2の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数 f2(y) の定義
f2_y = 6 * y_values * (1 - y_values)
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量の第2要素を抽出 (Y2)
Y2_samples = np.median(samples, axis=1) # 中央値
# 期待値の計算
expected_Y2 = np.mean(Y2_samples)
# 理論値との比較
theoretical_Y2 = 0.5 # 中央値
# 期待値を表示
print(f"シミュレーションによる E[Y2](中間値の期待値): {expected_Y2:.4f}, 理論値: {theoretical_Y2:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数 f2(y) のプロット
plt.plot(y_values, f2_y, label='$f_2(y) = 6y(1-y)$', color='red')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y2_samples, bins=50, density=True, alpha=0.5, color='red', label='Y2 samples (median)')
# グラフの設定
plt.title('確率密度関数 $f_2(y)$ とヒストグラム (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y2](中間値の期待値): 0.5006, 理論値: 0.5000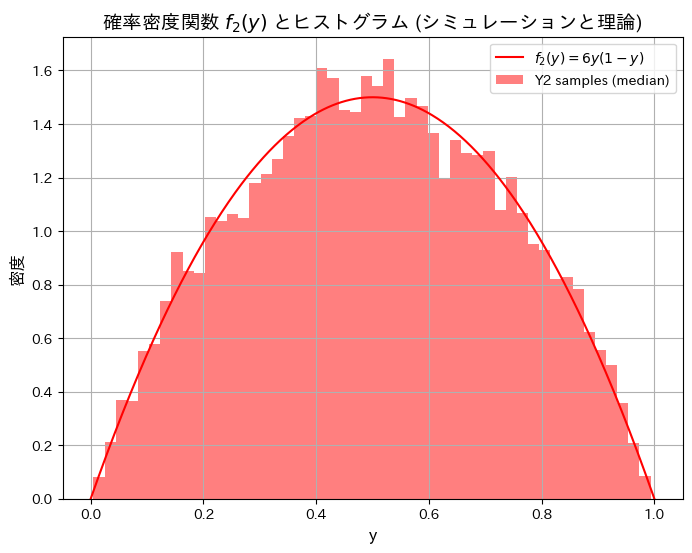
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
次に、Y1~Y3の確率密度関数と累積分布関数を重ねて見てみます。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f2_y = 6 * y_values * (1 - y_values)
f3_y = 3 * y_values ** 2
# CDF (累積分布関数) の計算
cdf1_y = np.cumsum(f1_y) * (y_values[1] - y_values[0])
cdf2_y = np.cumsum(f2_y) * (y_values[1] - y_values[0])
cdf3_y = np.cumsum(f3_y) * (y_values[1] - y_values[0])
# グラフの作成
plt.figure(figsize=(10, 8))
# 確率密度関数 (PDF) のプロット
plt.subplot(2, 1, 1)
plt.plot(y_values, f1_y, label='$f_1(y)$', color='blue')
plt.plot(y_values, f2_y, label='$f_2(y)$', color='red')
plt.plot(y_values, f3_y, label='$f_3(y)$', color='green')
plt.title('確率密度関数 (PDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# 累積分布関数 (CDF) のプロット
plt.subplot(2, 1, 2)
plt.plot(y_values, cdf1_y, label='$F_1(y)$', color='blue')
plt.plot(y_values, cdf2_y, label='$F_2(y)$', color='red')
plt.plot(y_values, cdf3_y, label='$F_3(y)$', color='green')
plt.title('累積分布関数 (CDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend(loc='lower right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()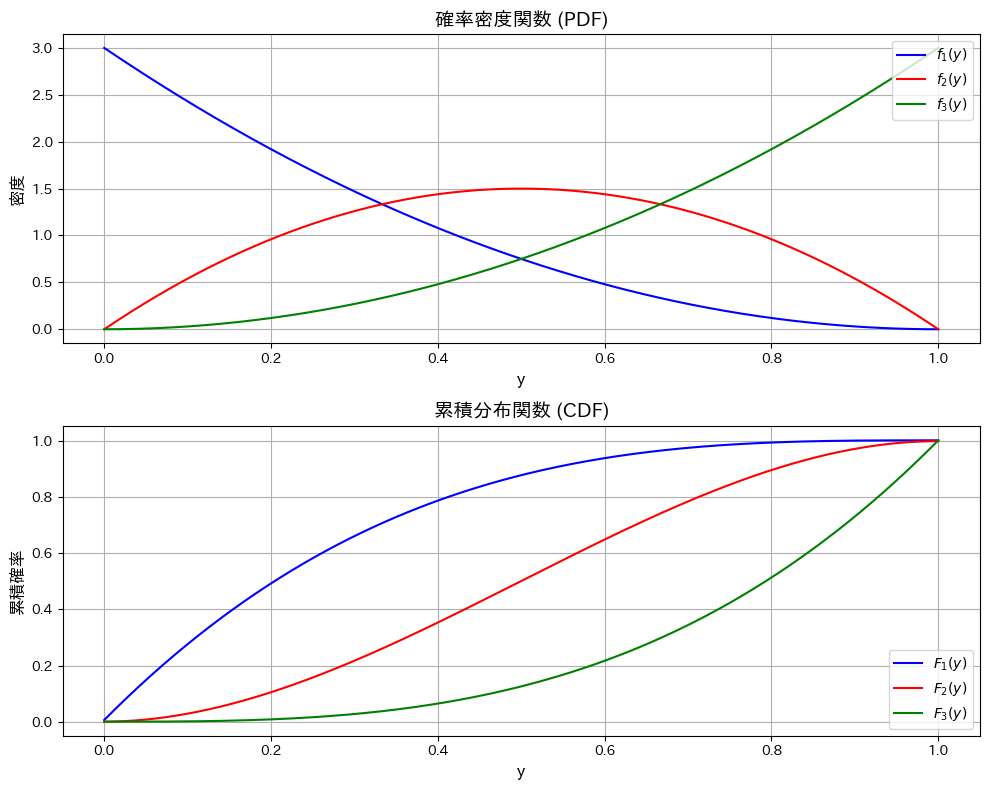
Y1は左寄り、Y2は中央寄り、Y3は右寄りになっていて、順序統計量の性質を直感的に表されています。Y2の確率密度関数は左右対称なので期待値が0.5になることも分かります。Y2の累積分布関数が直線でないことも面白いです。