二項分布の期待値と分散を求めました。
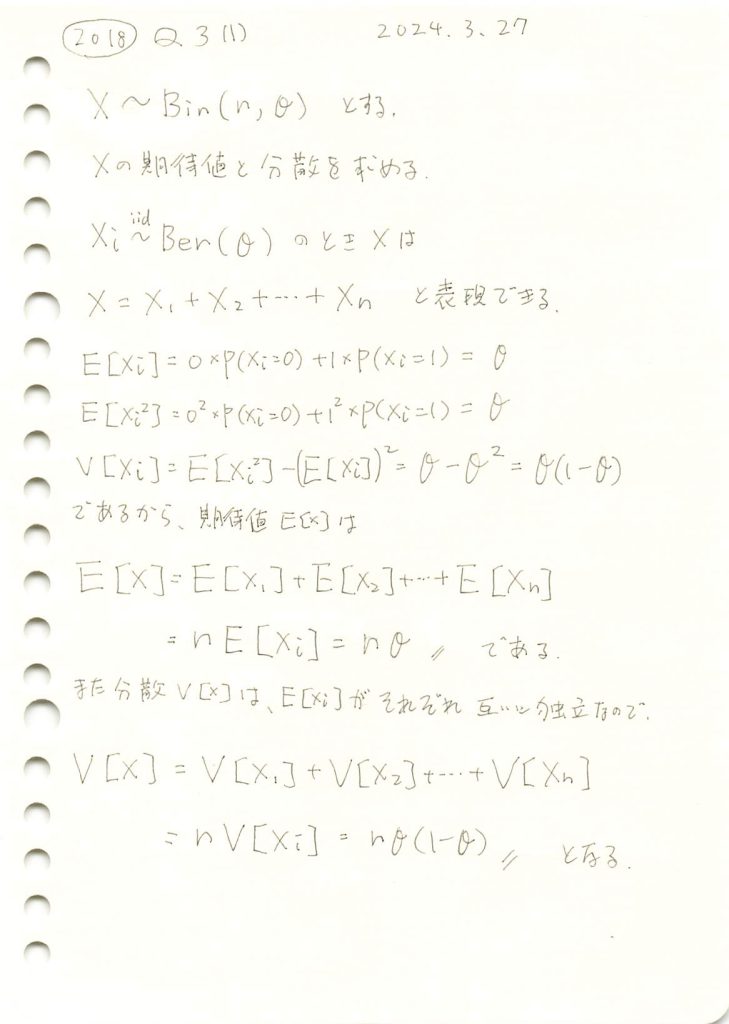
コード
ベルヌーイ試行による二項分布のシミュレーションを行い二項分布の期待値と分散を求めます。
# 2018 Q3(1) 2024.10.11
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 10000 # シミュレーションの回数
# シミュレーションを実行
bernoulli_trials = np.random.binomial(1, theta, (num_simulations, n))
# 各シミュレーションでの X = X1 + X2 + ... + Xn を計算
X_values = np.sum(bernoulli_trials, axis=1)
# 期待値と分散を計算
simulated_mean = np.mean(X_values)
simulated_variance = np.var(X_values)
# 理論値
theoretical_mean = n * theta
theoretical_variance = n * theta * (1 - theta)
# 結果を表示
print(f"シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の期待値: {theoretical_mean}")
print(f"シミュレーションによる分散: {simulated_variance}")
print(f"理論上の分散: {theoretical_variance}")
# ヒストグラムを描画
plt.hist(X_values, bins=np.arange(n+2)-0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
plt.title("ベルヌーイ試行による二項分布のシミュレーション")
plt.xlabel("Xの値 (成功回数)")
plt.ylabel("確率")
plt.show()シミュレーションによる期待値: 4.9827
理論上の期待値: 5.0
シミュレーションによる分散: 2.54300071
理論上の分散: 2.5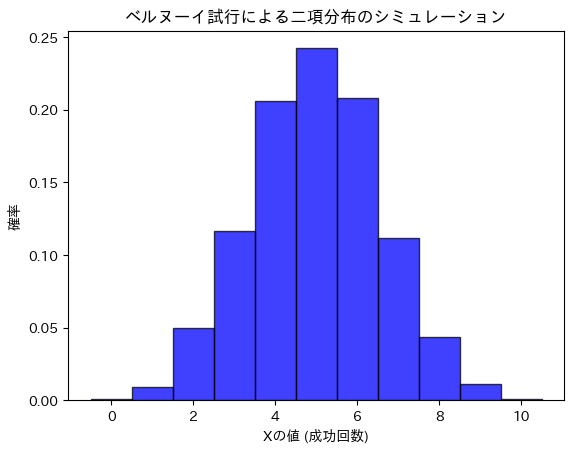
シミュレーションによる結果と理論値が一致しました。