漸近分散の相対標準偏差を求める問題をやりました。

コード
NとMを変化させてシミュレーションし![]() の分布を描画しました。
の分布を描画しました。![]() を求め、理論値と一致するか確認してみます。
を求め、理論値と一致するか確認してみます。
# 2018 Q2(5)-2 2024.10.10
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 1000 # 真の青球の数 N (これを推定する)
K_values = [100, 300, 500] # 赤球の数 K のバリエーション
n_values = [100, 200, 300] # 抽出する回数 n のバリエーション
n_trials = 10000 # シミュレーションの試行回数
# グラフレイアウト設定
fig, axes = plt.subplots(len(K_values), len(n_values), figsize=(15, 12))
axes = axes.flatten()
plot_idx = 0
# 各 K, n の組み合わせに対してシミュレーションを実行
for K in K_values:
for n in n_values:
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果から N_hat の分散を計算
N_hat_var = np.var(N_hat_values)
# 理論値 ε の計算
epsilon_theory = np.sqrt((N_true + K) * (N_true + K - n) / (n * N_true * K))
# シミュレーションから求めた ε の計算
epsilon_simulation = np.sqrt(N_hat_var) / N_true
# 推定量 N_hat の分布をヒストグラムで表示
ax = axes[plot_idx]
ax.hist(N_hat_values, bins=100, density=True, alpha=0.7, color='b', edgecolor='black')
ax.axvline(x=N_true, color='r', linestyle='--') # 真の N を破線で表示
ax.set_title(f'K={K}, n={n}')
ax.set_xlabel('推定量 N_hat')
ax.set_ylabel('確率密度')
# εの値と真のNをまとめて表示
ax.text(0.95, 0.95, f'真の N = {N_true}\nε (理論) = {epsilon_theory:.4f}\nε (シミュ) = {epsilon_simulation:.4f}',
transform=ax.transAxes, verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', alpha=0.7), fontsize=10)
ax.grid(True)
plot_idx += 1
# グラフ全体の調整
plt.tight_layout()
plt.show()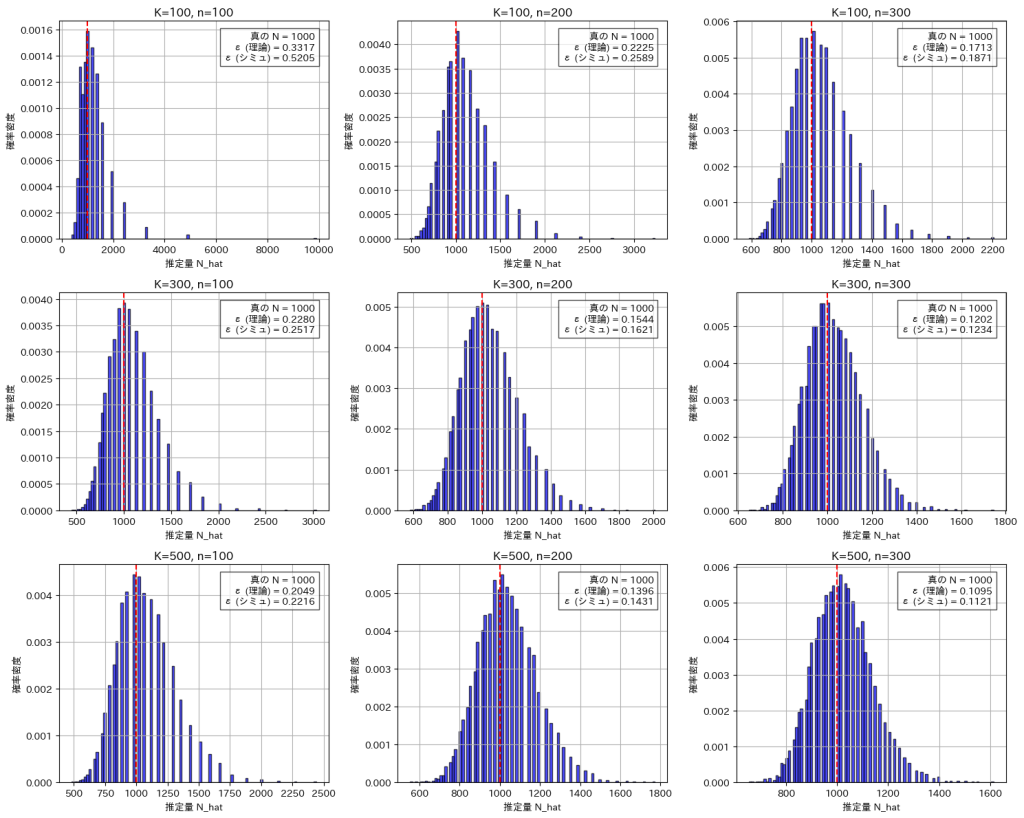
シミュレーションによる結果は理論値と概ね一致しました。