カイ二乗分布の分散を求めました。
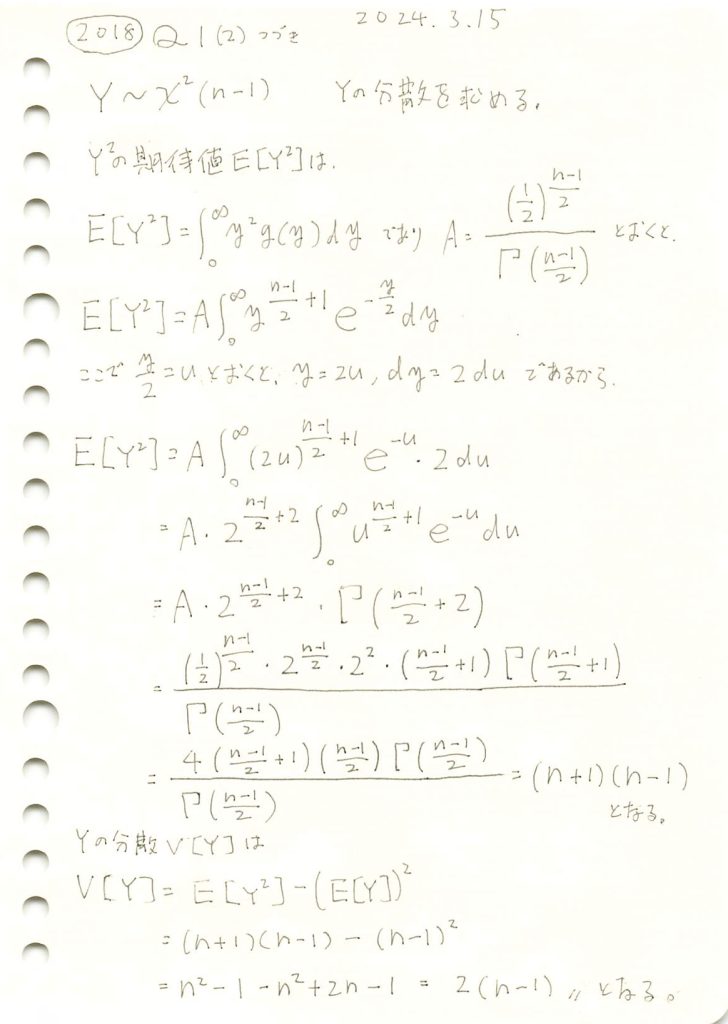
コード
数値シミュレーションにより、n=10(自由度9)のカイ二乗分布の期待値と分散を求めてみます。
# 2018 Q1(2) 2024.10.2
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # サンプルサイズ (自由度は n-1)
degrees_of_freedom = n - 1 # 自由度
num_simulations = 10000 # シミュレーションの回数
# カイ二乗分布に従うランダム変数を生成
chi_squared_samples = np.random.chisquare(df=degrees_of_freedom, size=num_simulations)
# 期待値と分散を計算
empirical_mean = np.mean(chi_squared_samples)
empirical_variance = np.var(chi_squared_samples)
# 理論値
theoretical_mean = degrees_of_freedom # 期待値 E[Y] = n-1
theoretical_variance = 2 * degrees_of_freedom # 分散 Var(Y) = 2(n-1)
# 結果表示
print(f"カイ二乗分布の期待値 (理論): {theoretical_mean:.4f}")
print(f"カイ二乗分布の期待値 (シミュレーション): {empirical_mean:.4f}")
print(f"カイ二乗分布の分散 (理論): {theoretical_variance:.4f}")
print(f"カイ二乗分布の分散 (シミュレーション): {empirical_variance:.4f}")
# ヒストグラムを描画して確認
plt.hist(chi_squared_samples, bins=50, alpha=0.7, color='b', edgecolor='black')
plt.axvline(empirical_mean, color='r', linestyle='dashed', linewidth=2, label='シミュレーション平均')
plt.axvline(theoretical_mean, color='g', linestyle='dashed', linewidth=2, label='理論平均')
plt.title('カイ二乗分布 (自由度 10-1)')
plt.xlabel('値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()カイ二乗分布の期待値 (理論): 9.0000
カイ二乗分布の期待値 (シミュレーション): 8.9728
カイ二乗分布の分散 (理論): 18.0000
カイ二乗分布の分散 (シミュレーション): 18.3530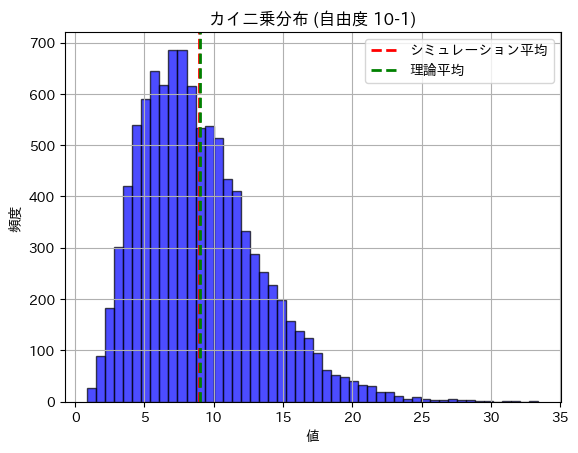
期待値と分散は理論値に近い値になりました。