線形関係のある確率変数の条件付き確率分布を求めました。

コード
X|Z=zが![]() に従うかシミュレーションし確かめます。
に従うかシミュレーションし確かめます。
# 2017 Q4(4) 2024.11.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 1000000
z_fixed = 3 # 条件として与える Z の値
# シミュレーション
Y = np.random.normal(0, 1, num_samples)
X = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# Z = z_fixed に条件を付けた X の分布を抽出
X_given_Z = (X[np.abs(Z - z_fixed) < 0.05])
# 理論値の計算
mean_conditional = (k / (k**2 + 1)) * (z_fixed - a)
std_dev_conditional = np.sqrt(1 / (k**2 + 1))
# シミュレーションによる値の計算
mean_simulation = np.mean(X_given_Z)
std_dev_simulation = np.std(X_given_Z)
# 理論値とシミュレーション値を出力
print(f"理論上の期待値 (X | Z = {z_fixed}): {mean_conditional}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_conditional}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# 条件付き分布のヒストグラム
plt.hist(X_given_Z, bins=50, density=True, alpha=0.6, color='b', label=f"シミュレーション X | Z = {z_fixed}")
# 理論分布をプロット
x_vals = np.linspace(min(X_given_Z), max(X_given_Z), 100)
plt.plot(x_vals, norm.pdf(x_vals, mean_conditional, std_dev_conditional), 'r', label="理論分布")
# グラフの装飾
plt.title(f"条件付き分布 X | Z = {z_fixed}")
plt.xlabel("X の値")
plt.ylabel("密度")
plt.legend()
plt.show()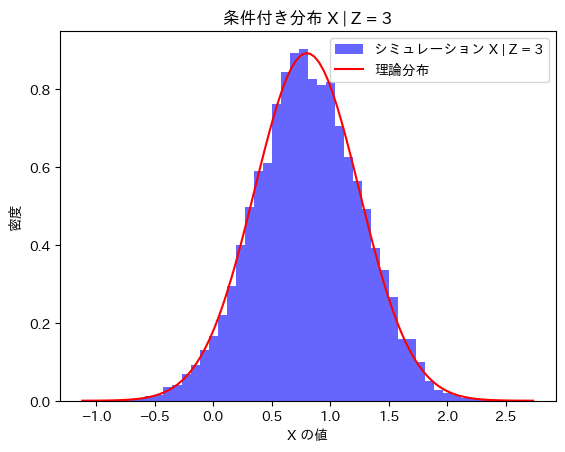
X|Z=zは![]() に従うことが確認できました。
に従うことが確認できました。