ポアソン分布に従う独立した2変数の和の分布を3つの方法で求めました。
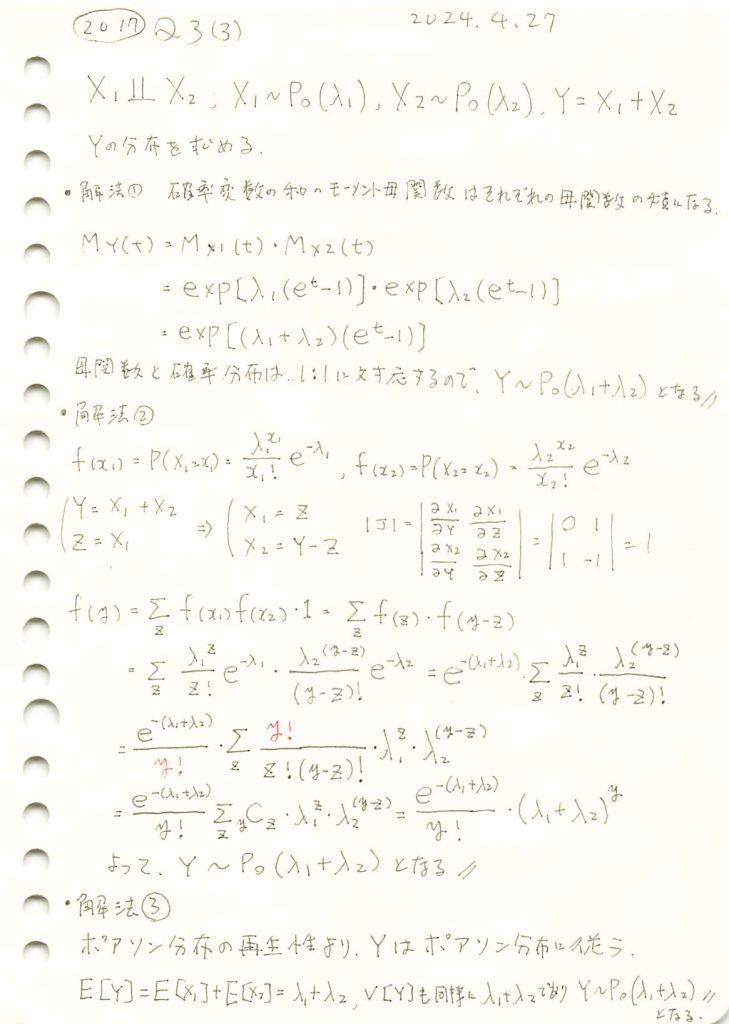
コード
ポアソン分布に従う独立した2変数X1,X2と、Y=X1+X2の分布をシミュレーションしました。
# 2017 Q3(3) 2024.11.4
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_1 = 3 # X1のポアソン分布のパラメータ
lambda_2 = 4 # X2のポアソン分布のパラメータ
sample_size = 10000 # サンプルサイズ
# X1 と X2 のサンプルを生成
X1_samples = np.random.poisson(lambda_1, sample_size)
X2_samples = np.random.poisson(lambda_2, sample_size)
Y_samples = X1_samples + X2_samples # Y = X1 + X2 のサンプル
# ヒストグラムをプロット (塗りあり)
plt.figure(figsize=(10, 4.2)) # 高さを70%に縮小
plt.hist(X1_samples, bins=range(0, 20), density=True, alpha=0.5, label=f"X1 ~ ポアソン(λ1 = {lambda_1})", color="blue")
plt.hist(X2_samples, bins=range(0, 20), density=True, alpha=0.5, label=f"X2 ~ ポアソン(λ2 = {lambda_2})", color="green")
plt.hist(Y_samples, bins=range(0, 20), density=True, alpha=0.5, label=f"Y = X1 + X2 ~ ポアソン(λ1 + λ2 = {lambda_1 + lambda_2})", color="red", histtype='stepfilled')
# ヒストグラムのカスタマイズ
plt.xlabel("値")
plt.ylabel("確率密度")
plt.title("ポアソン分布の重ね合わせ (X1, X2, および Y = X1 + X2)")
plt.legend()
plt.grid(True)
plt.show()
# CDFの計算用にPMFを求める
x_values = range(0, 20)
pmf_X1 = [np.exp(-lambda_1) * lambda_1**x / np.math.factorial(x) for x in x_values]
pmf_X2 = [np.exp(-lambda_2) * lambda_2**x / np.math.factorial(x) for x in x_values]
pmf_Y = [np.exp(-(lambda_1 + lambda_2)) * (lambda_1 + lambda_2)**x / np.math.factorial(x) for x in x_values]
# CDFを計算
X1_cdf = np.cumsum(pmf_X1)
X2_cdf = np.cumsum(pmf_X2)
Y_cdf = np.cumsum(pmf_Y)
# CDFのプロット
plt.figure(figsize=(10, 4.2))
plt.step(x_values, X1_cdf, where='mid', label=f"X1 ~ ポアソン(λ1 = {lambda_1}) CDF", color="blue")
plt.step(x_values, X2_cdf, where='mid', label=f"X2 ~ ポアソン(λ2 = {lambda_2}) CDF", color="green")
plt.step(x_values, Y_cdf, where='mid', label=f"Y = X1 + X2 ~ ポアソン(λ1 + λ2 = {lambda_1 + lambda_2}) CDF", linestyle="--", color="red")
# CDFプロットのカスタマイズ
plt.xlabel("値")
plt.ylabel("累積分布関数 (CDF)")
plt.title("ポアソン分布の累積分布関数 (X1, X2, および Y = X1 + X2)")
plt.legend()
plt.grid(True)
plt.show()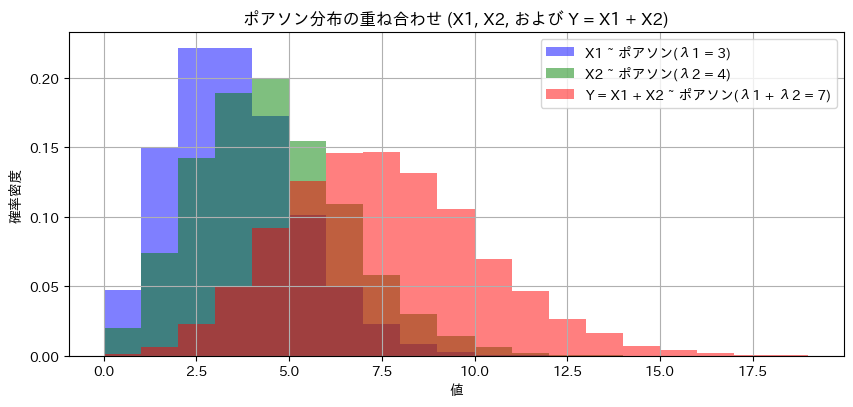
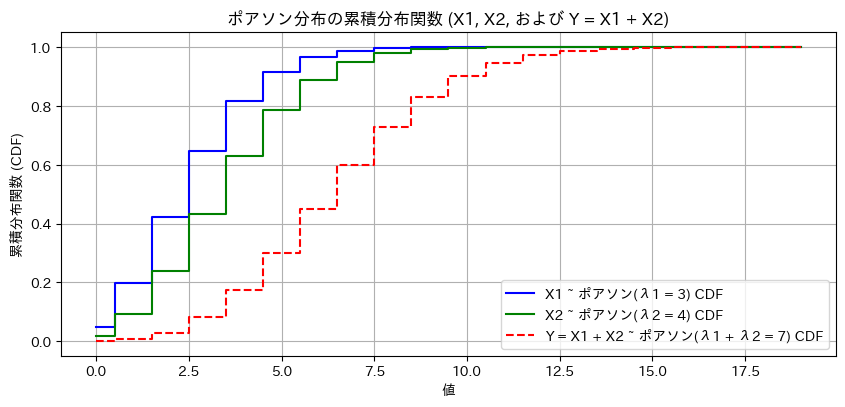
X1~Po(λ1),X1~Po(λ2)のときY=X1+X2~Po(λ1+λ2)になることをグラフの形状からも確認できました。