二項分布の極限をとってポアソン分布を導出しました。
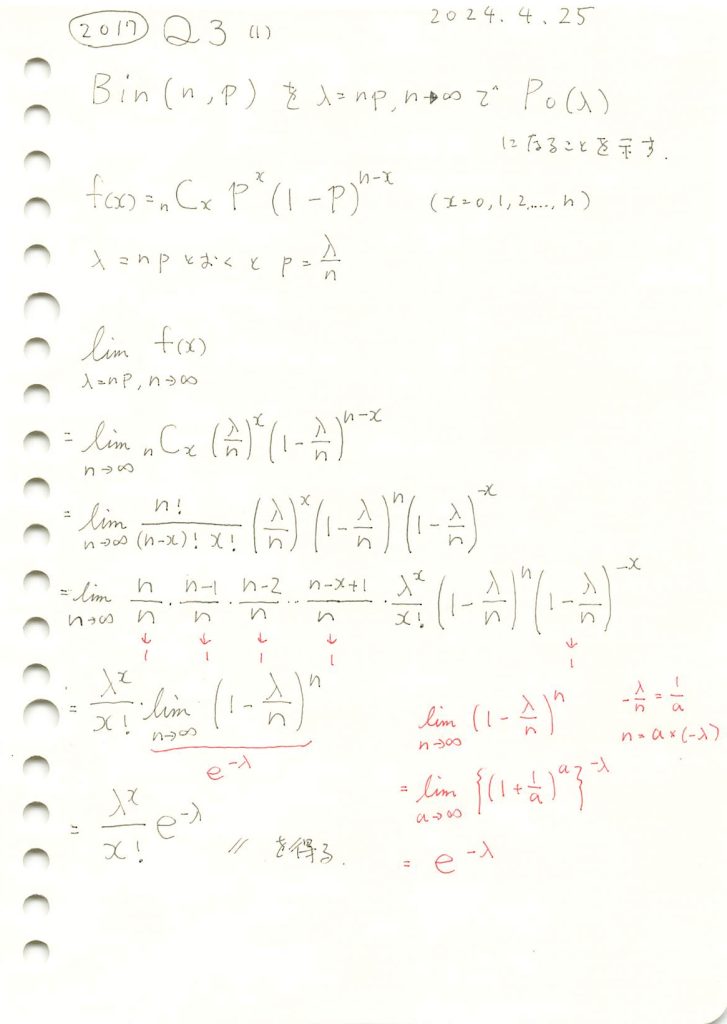
λ=5に固定しnを徐々に増加させて二項分布がポアソン分布に近づくのか確認してみます。
# 2017 Q3(1) 2024.11.2
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
lambda_value = 5 # ポアソン分布の λ
n_values = [10, 50, 100, 500, 1000] # 二項分布の異なる n 値
sample_size = 10000 # サンプル数
# サブプロットの設定
fig, axes = plt.subplots(len(n_values), 1, figsize=(8, len(n_values) * 3))
fig.suptitle("二項分布の極限がポアソン分布に収束")
# 各 n に対するシミュレーションとプロット
for i, n in enumerate(n_values):
p = lambda_value / n # 与えられた λ に対する p の計算
binomial_samples = np.random.binomial(n, p, sample_size) # 二項分布のサンプル
poisson_samples = np.random.poisson(lambda_value, sample_size) # ポアソン分布のサンプル(比較用)
# ヒストグラムのプロット
axes[i].hist(binomial_samples, bins=range(0, 20), alpha=0.5, label=f"二項分布(n={n}, p={p:.3f})", density=True)
axes[i].hist(poisson_samples, bins=range(0, 20), alpha=0.5, label=f"ポアソン分布(λ={lambda_value})", density=True)
axes[i].legend()
axes[i].set_xlabel("x")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"n = {n}, p = {p:.5f}")
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()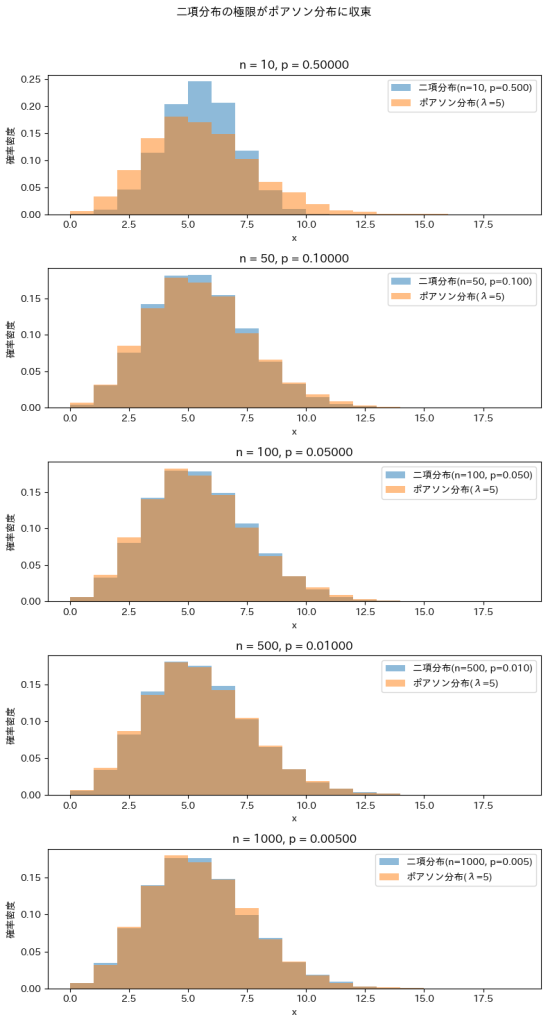
nが大きくなるにつれて二項分布はポアソン分布に近づくのが確認できました。