標本平均の2倍が一様分布の上限値の不偏推定量であることの証明をしました。

コード
θ=10,n=20としてシミュレーションを行い、θ’の分布を見てみます。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ' の分布をヒストグラムで表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\' = 2\bar{X}$')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2\bar{X}$ の分布')
plt.legend()
plt.show()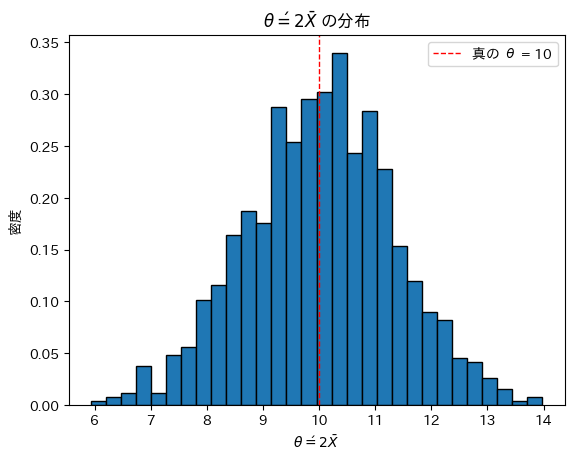
θ’は真のθを中心に左右対称にバラついています。θ’は不偏であるように見えます。
次にサンプルサイズnを変化させて不偏推定量θ’がどうなるのか確認をします。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' の平均を記録
theta_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# 各 n に対する θ' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\' = 2 \bar{X}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\' = 2 \bar{X}$ の関係')
plt.legend()
plt.show()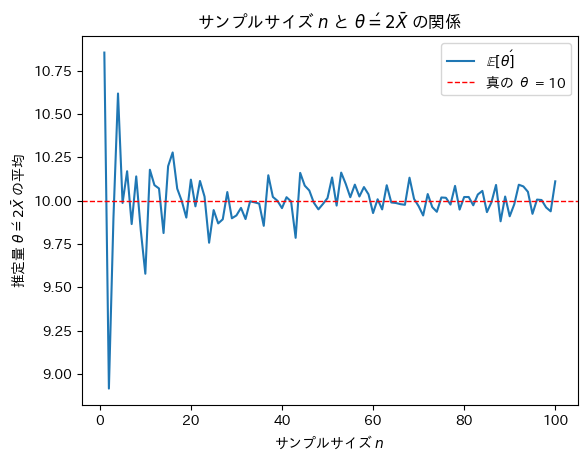
サンプルサイズnが増加するにつれて不偏推定量θ’は真のθに近づくことが確認できました。