この前と同じ問ですが、解き方が間違っていたので、再チャレンジです。
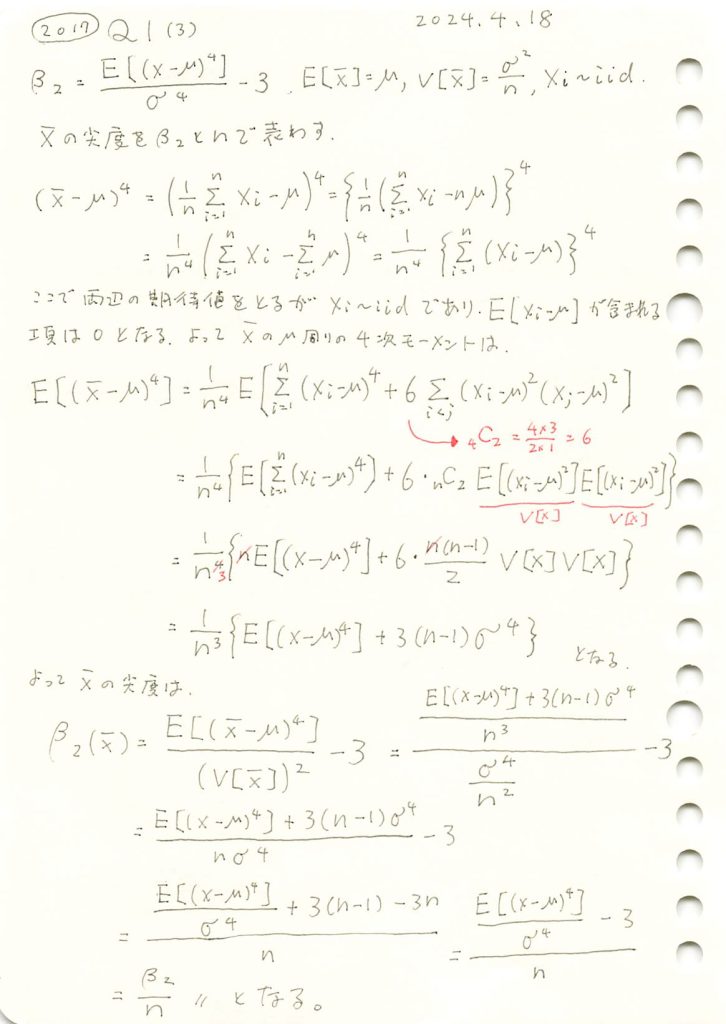
コード
Xの標本平均の尖度(過剰尖度)が![]() になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
# 2017 Q1(3) 2024.10.26
from scipy.stats import kurtosis, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
num_simulations = 30000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 110, 10) # サンプルサイズの設定
# 尖度を持つ母集団分布としてガンマ分布を使用(shape=2で正の尖度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# 理論的な過剰尖度(ガンマ分布の尖度の計算)
beta_2_theoretical = 6 / shape_param # ガンマ分布の過剰尖度
# シミュレーション結果を保存するリスト
sample_mean_excess_kurtosis = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
kurt_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
kurt_values.append(sample_mean)
# 標本平均の尖度を計算し、過剰尖度に変換(-3)
kurtosis_of_sample_mean = kurtosis(kurt_values, fisher=False) - 3 # 尖度を計算し、過剰尖度に変換
sample_mean_excess_kurtosis.append(kurtosis_of_sample_mean)
# 理論値の計算
theoretical_excess_kurtosis = [beta_2_theoretical / n for n in sample_sizes]
# グラフの作成
plt.figure(figsize=(10, 6))
# シミュレーション結果のプロット
plt.plot(sample_sizes, sample_mean_excess_kurtosis, marker='o', label='シミュレーション結果 (過剰尖度)')
plt.plot(sample_sizes, theoretical_excess_kurtosis, color='r', linestyle='--', label='理論値: $\\frac{\\beta_2}{n}$')
plt.title('$\\bar{X}$ の過剰尖度のシミュレーションと理論値の比較')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$\\bar{X}$ の過剰尖度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()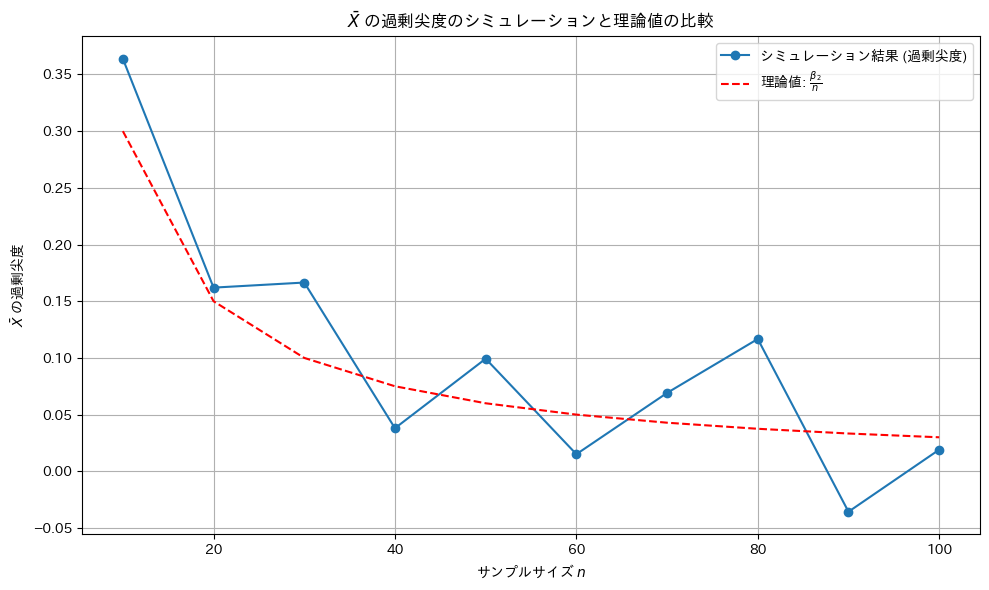
尖度は理論値に沿うものの、歪度(前問)より更に外れ値の影響を受けやすいため分散が大きい。
シミュレーション回数を10倍にしてみます。
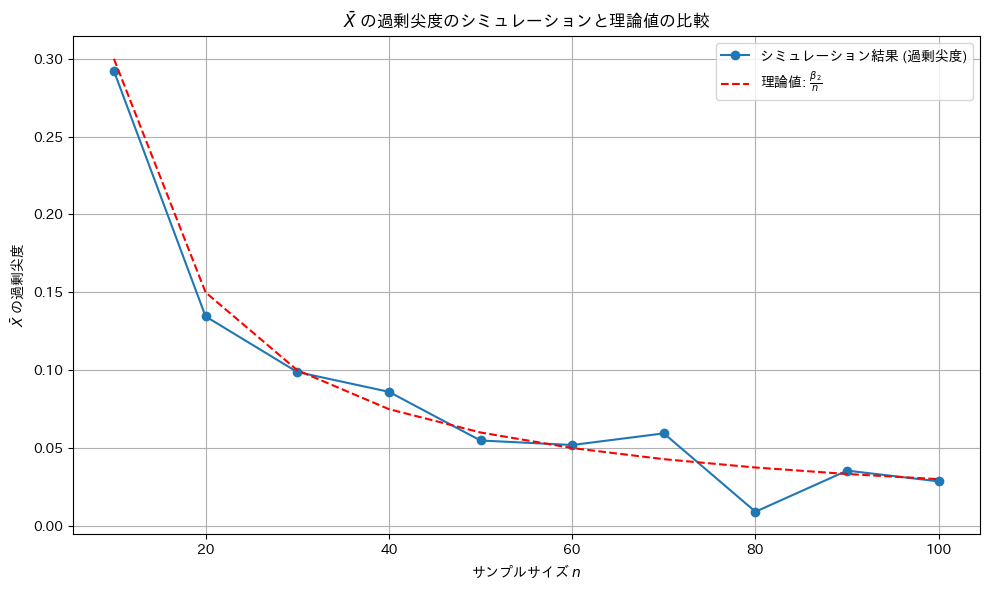
尖度は理論値に近づきました。