欠測のメカニズムがMCARであるか検定する手法の有効性について学びました。

コード
MCARと非MCARの場合の![]() の分布を、棄却域とともに描画をしてみます。
の分布を、棄却域とともに描画をしてみます。
# 2016 Q5(4) 2024.11.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f
# シミュレーションパラメータ
n = 100 # 全サンプル数
m = 60 # 観測可能なデータ数
repeats = 1000 # シミュレーション回数
alpha = 0.05 # 有意水準
# F分布の上位5%点を計算
df1 = 1 # F分布の分子自由度
df2 = n - 2 # F分布の分母自由度
F_critical = f.ppf(1 - alpha, dfn=df1, dfd=df2)
# d^2 の上位5%点を計算
d2_critical = (n - 1) * F_critical / (n - 2 + F_critical)
# MCARデータの生成
def generate_mcar_data(n, m):
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)
observed_indices = np.random.choice(n, m, replace=False) # ランダムにm個観測
X_obs, Y_obs = X[observed_indices], Y[observed_indices]
X_miss = np.delete(X, observed_indices) # 欠測部分
return X_obs, X_miss
# MCARではないデータの生成 (欠測がXに依存)
def generate_non_mcar_data(n, m):
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)
# ロジスティック関数を使用して、全実数を0~1の確率に変換
prob = 1 / (1 + np.exp(-X)) # Xに依存した欠測確率
observed_indices = np.random.choice(n, m, replace=False, p=prob / prob.sum())
X_obs, Y_obs = X[observed_indices], Y[observed_indices]
X_miss = np.delete(X, observed_indices) # 欠測部分
return X_obs, X_miss
# d^2 の計算
def calculate_d2(X_obs, X_miss):
n = len(X_obs) + len(X_miss)
m = len(X_obs)
X_bar = np.mean(np.concatenate([X_obs, X_miss]))
X_obs_bar = np.mean(X_obs)
X_miss_bar = np.mean(X_miss)
S2 = np.var(np.concatenate([X_obs, X_miss]), ddof=1)
d2 = (1 / S2) * (m * (X_obs_bar - X_bar)**2 + (n - m) * (X_miss_bar - X_bar)**2)
return d2
# MCARデータと非MCARデータで帰無仮説を棄却した割合を計算
results_mcar = [calculate_d2(*generate_mcar_data(n, m)) > d2_critical for _ in range(repeats)]
results_non_mcar = [calculate_d2(*generate_non_mcar_data(n, m)) > d2_critical for _ in range(repeats)]
# 結果を出力
mcar_rejection_rate = np.mean(results_mcar) * 100 # 棄却率 (%)
non_mcar_rejection_rate = np.mean(results_non_mcar) * 100 # 棄却率 (%)
print(f"MCARデータで帰無仮説を棄却した割合: {mcar_rejection_rate:.2f}%")
print(f"非MCARデータで帰無仮説を棄却した割合: {non_mcar_rejection_rate:.2f}%")
# MCARデータと非MCARデータのd^2値を収集
d2_values_mcar = [calculate_d2(*generate_mcar_data(n, m)) for _ in range(repeats)]
d2_values_non_mcar = [calculate_d2(*generate_non_mcar_data(n, m)) for _ in range(repeats)]
# 理論的なd^2の曲線を計算するためのx軸範囲を設定
x_theoretical = np.linspace(0, max(max(d2_values_mcar), max(d2_values_non_mcar)), 500)
# d^2の理論的な確率密度関数を計算
d2_pdf_theoretical = f.pdf(x_theoretical * (n - 2) / (n - 1 - x_theoretical), dfn=df1, dfd=df2)
scaling_factor = (n - 2) / (n - 1)
d2_pdf_theoretical *= scaling_factor
# ヒストグラムの可視化
plt.figure(figsize=(12, 6))
# MCARデータのヒストグラム
plt.hist(d2_values_mcar, bins=30, alpha=0.7, label="MCARデータ", color="blue", density=True)
# 非MCARデータのヒストグラム
plt.hist(d2_values_non_mcar, bins=30, alpha=0.7, label="非MCARデータ", color="orange", density=True)
# 理論的な曲線をプロット
plt.plot(x_theoretical, d2_pdf_theoretical, label="理論的な $d^2$ 分布", color="green", linewidth=2)
# 臨界値をラインで表示
plt.axvline(d2_critical, color="red", linestyle="--", label=r"$d^2$ の臨界値", linewidth=2)
# グラフの装飾
plt.title(r"$d^2$ の分布と理論曲線: MCAR vs 非MCAR", fontsize=14)
plt.xlabel(r"$d^2$ の値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# x軸の範囲を制限
plt.xlim(0, 20)
plt.tight_layout()
plt.show()MCARデータで帰無仮説を棄却した割合: 4.10%
非MCARデータで帰無仮説を棄却した割合: 91.70%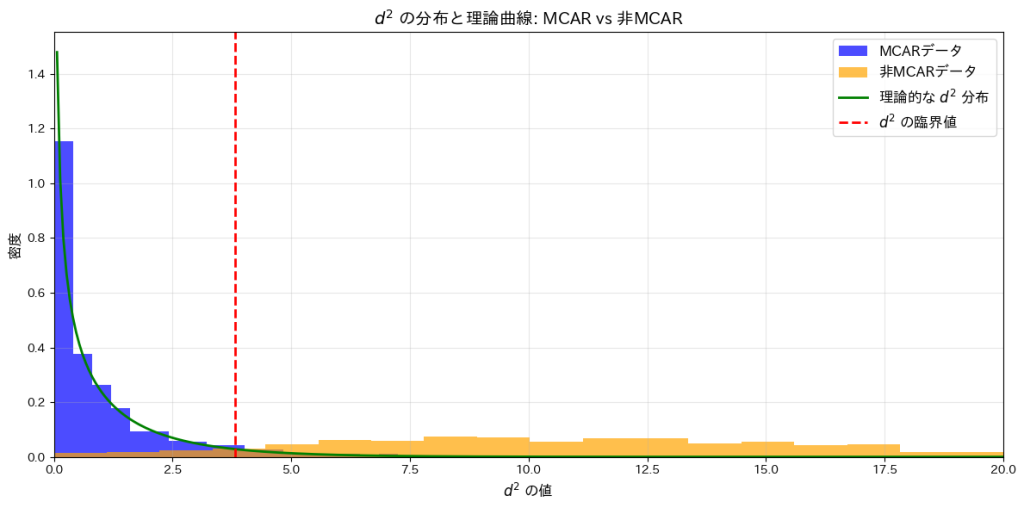
これらの結果から、有意水準を基準にした検定がMCARと非MCARの違いを正確に識別できることが確認されました。
次に、分散の違いを検出するため、非MCARの観測データと欠測データについてF検定を実施します。分布を可視化するとともに、F値とp値を計算して結果を確認します。
# 2016 Q5(5) 2024.12.1
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f
# データ生成関数
def generate_non_mcar_data(n, m):
"""非MCARデータ生成: Xに依存して欠測"""
X = np.random.normal(0, 1, n) # 母集団は正規分布
Y = np.random.normal(0, 1, n) # ただし今回は使用しない
prob = 1 / (1 + np.exp(-5 * X)) # 欠測確率 (Xに依存)
observed_indices = np.random.choice(n, m, replace=False, p=prob / prob.sum())
X_obs = X[observed_indices]
X_miss = np.delete(X, observed_indices)
return X_obs, X_miss
# パラメータ設定
n = 100 # 全体のサンプル数
m = 60 # 観測されるサンプル数
# 非MCARデータ生成
X_obs, X_miss = generate_non_mcar_data(n, m)
# 平均と分散の計算
mean_obs = np.mean(X_obs)
var_obs = np.var(X_obs, ddof=1)
mean_miss = np.mean(X_miss)
var_miss = np.var(X_miss, ddof=1)
# F検定
F_statistic = var_obs / var_miss # F値
df1 = m - 1 # 観測データの自由度
df2 = n - m - 1 # 欠測データの自由度
p_value = 2 * min(f.cdf(F_statistic, df1, df2), 1 - f.cdf(F_statistic, df1, df2))
# 結果の表示
print(f"観測データの平均: {mean_obs:.5f}, 分散: {var_obs:.5f}")
print(f"欠測データの平均: {mean_miss:.5f}, 分散: {var_miss:.5f}")
print(f"F値: {F_statistic:.5f}")
print(f"p値: {p_value:.5f}")
# 可視化
plt.figure(figsize=(12, 6))
# ヒストグラムをプロット
plt.hist(X_obs, bins=15, alpha=0.7, label=f"観測データ (平均: {mean_obs:.2f}, 分散: {var_obs:.2f})", color="blue", density=True)
plt.hist(X_miss, bins=15, alpha=0.7, label=f"欠測データ (平均: {mean_miss:.2f}, 分散: {var_miss:.2f})", color="orange", density=True)
# グラフ設定
plt.title("非MCARの観測データと欠測データの分布", fontsize=14)
plt.xlabel("値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend(fontsize=10)
plt.grid(alpha=0.3)
plt.show()観測データの平均: 0.67735, 分散: 0.55682
欠測データの平均: -0.88573, 分散: 0.46808
F値: 1.18958
p値: 0.57003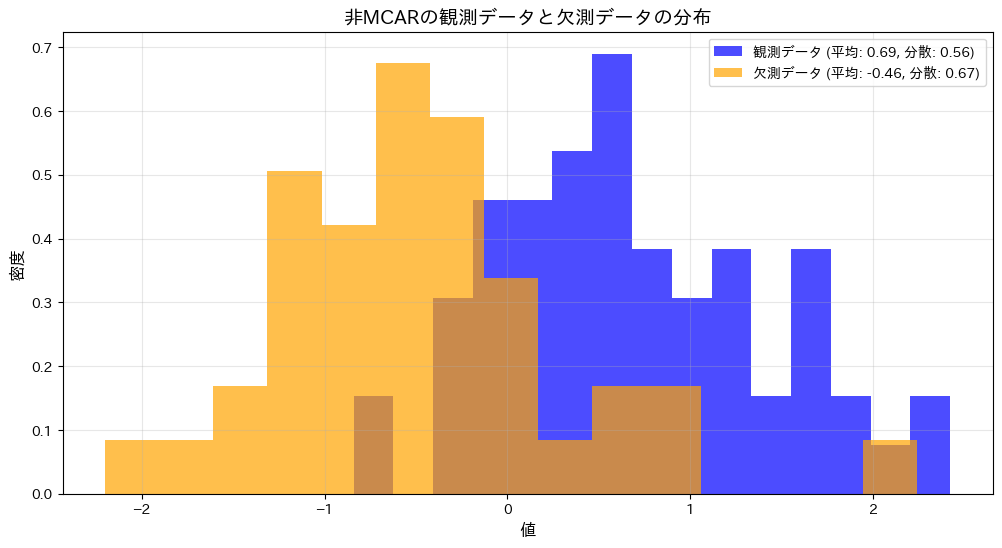
p値0.57003は有意水準を大きく上回り、非MCARの観測データと欠測データの分散に統計的な差があるとは言えません。また、グラフからも両者のばらつきに大きな違いがないことが視覚的に確認されました。