線形モデルの未知の母数βの3つの不偏推定量の各分散を求めました。
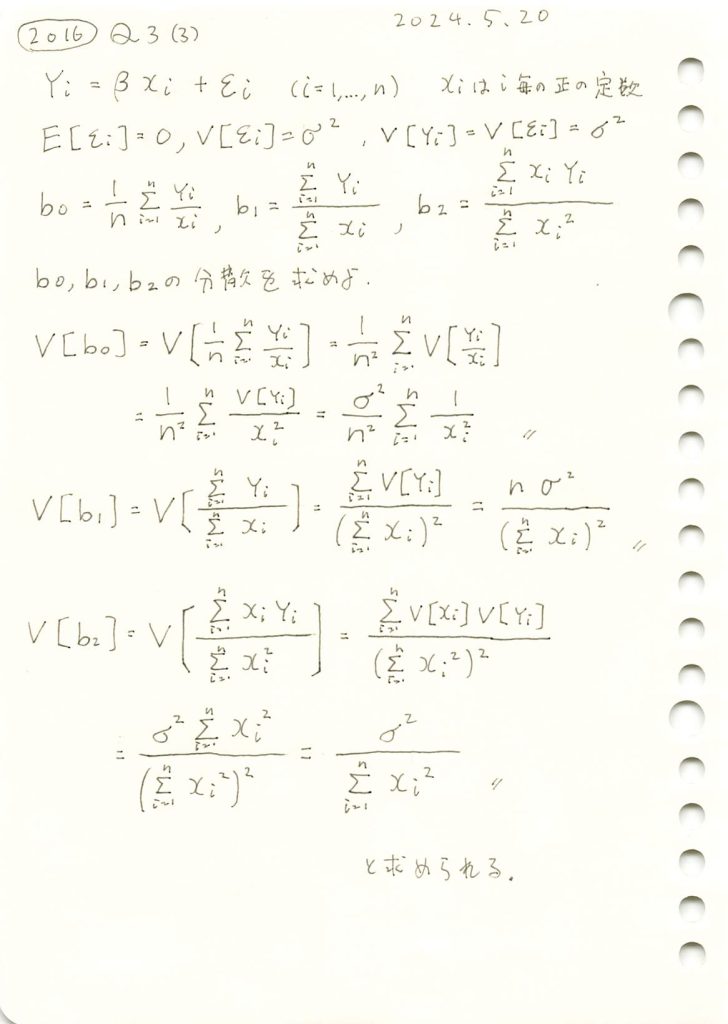
コード
線形モデルのパラメータβの推定量b0,b1,b2の分散の違いを理論式に基づいて確認します。説明変数xiには一様分布に従う値を与え、サンプル数nを変化させて、各推定量の分散の変化を視覚的に比較してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, variances_b0, label='$V[b_0]$', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, variances_b1, label='$V[b_1]$', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, variances_b2, label='$V[b_2]$', marker='s', linestyle='dashed', color='purple')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('分散')
plt.title('推定量 $b_0$, $b_1$, $b_2$ の理論的分散')
plt.legend()
plt.grid(True)
plt.show()
推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量であることが確認できました。
推定量b1,b2が重なっていて見えづらいため、標準誤差でも視覚化してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# 理論値からの標準偏差として各分散の平方根を計算
std_b0 = np.sqrt(variances_b0)
std_b1 = np.sqrt(variances_b1)
std_b2 = np.sqrt(variances_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, std_b0, label='$|b_0 - \\beta|$ (標準偏差)', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, std_b1, label='$|b_1 - \\beta|$ (標準偏差)', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, std_b2, label='$|b_2 - \\beta|$ (標準偏差)', marker='s', linestyle='dashed', color='purple')
plt.axhline(y=0, color='green', linestyle='solid', label='真の値 $\\beta = 2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('真の値からの標準偏差')
plt.title('推定量 $b_0, b_1, b_2$ の真の値からのずれ(標準偏差)')
plt.legend()
plt.grid(True)
plt.show()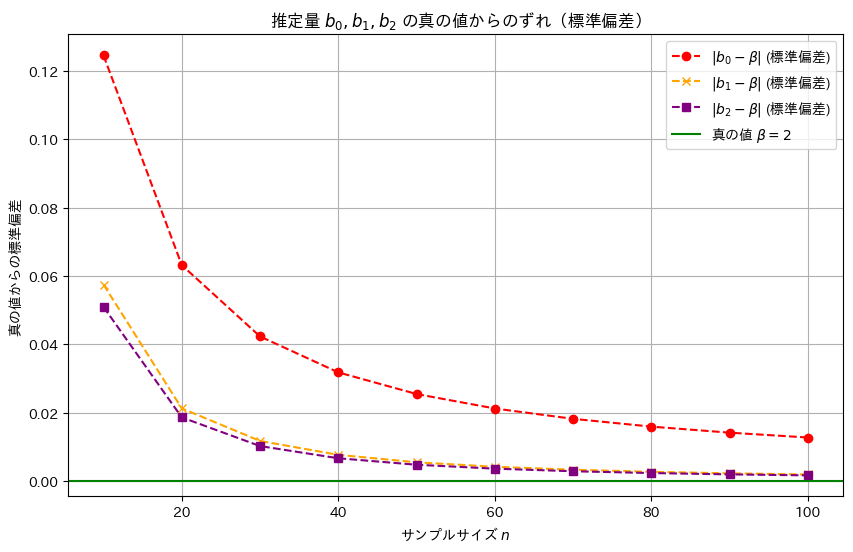
推定量b2,b1,b0の順に標準誤差は小さく、分散も同様の順序で小さくなることが確認できました。この結果から、最小二乗推定量b2が最も効率的であり、推定の安定性が高いことが再確認できました。