標準正規分布に従う確率変数の、右半分の条件付期待値を求めました。

コード
標準正規分布に従う確率変数 Zについて、条件付き期待値![]() になることをシミュレーションで確認をします。
になることをシミュレーションで確認をします。
# 2015 Q5(4) 2024.12.25
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーションパラメータ
num_samples = 100000 # サンプル数
# 標準正規分布からサンプルを生成
samples = np.random.normal(0, 1, num_samples)
# 条件 Z >= 0 のサンプルを抽出
samples_positive = samples[samples >= 0]
# 条件付き期待値のシミュレーション値
simulated_mean = np.mean(samples_positive)
# 理論値
theoretical_mean = np.sqrt(2 / np.pi)
# ヒストグラムの準備
x = np.linspace(-3, 3, 500) # x軸の範囲
pdf = norm.pdf(x) # 標準正規分布のPDF
# グラフの描画
plt.figure(figsize=(10, 6))
# 正規分布のPDF
plt.plot(x, pdf, label="標準正規分布のPDF", color="blue", linewidth=2)
# 条件 Z >= 0 のサンプルのヒストグラム
plt.hist(samples_positive, bins=50, density=True, alpha=0.6, color="orange", label="条件 Z ≧ 0 のシミュレーション")
# 結果の表示
plt.axvline(simulated_mean, color="green", linestyle="--", label=f"シミュレーション期待値: {simulated_mean:.4f}")
plt.axvline(theoretical_mean, color="red", linestyle="--", label=f"理論期待値: {theoretical_mean:.4f}")
# グラフの設定
plt.title("条件付き期待値の確認 (Z ≧ 0)", fontsize=14)
plt.xlabel("Z の値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.legend(fontsize=10)
plt.grid(True)
# グラフを表示
plt.tight_layout()
plt.show()
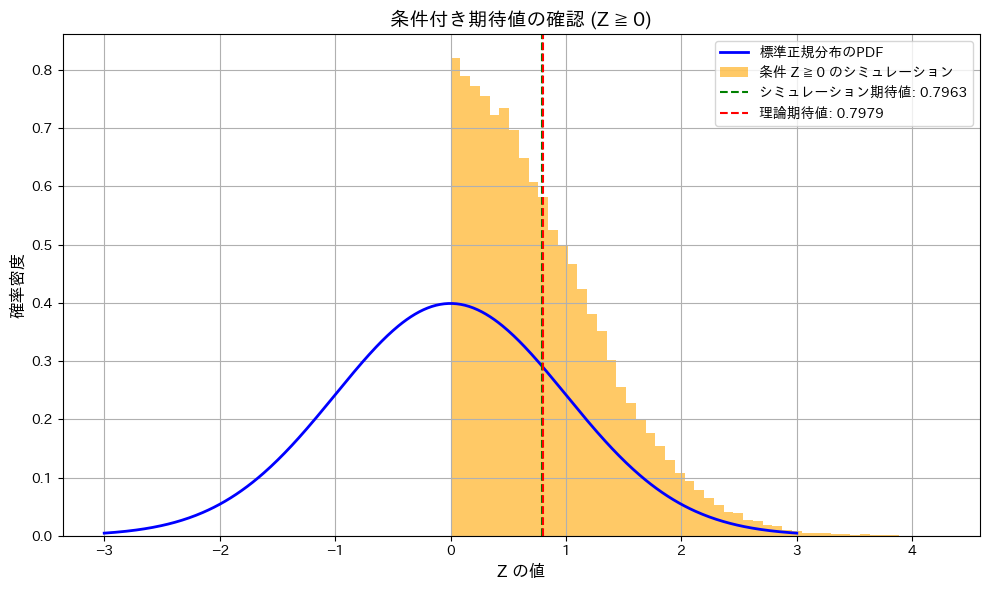
条件付き期待値![]() であることが確認されました。
であることが確認されました。