重回帰モデルの重みの2種類の推定量のMSEを求め比較しました。

コード
![]() を
を ![]() と
と ![]() の変化に対してプロットし、その符号の変化を確認します。
の変化に対してプロットし、その符号の変化を確認します。
# 2015 Q3(4) 2024.12.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_squared_vals = np.linspace(0, 0.99, 50) # r12^2の値(0から0.99まで)
beta2_squared_vals = np.linspace(0, 1.5, 50) # β2^2の値(0から1.5まで)
sigma2 = 1 # 誤差分散 σ^2
S11 = 10 # S11の仮定値
S12 = 5 # S12の仮定値
S22 = 15 # S22の仮定値
# グリッド生成
R12_squared, Beta2_squared = np.meshgrid(r12_squared_vals, beta2_squared_vals)
# MSEの差の計算
Var_beta2_hat = (sigma2 / S22) * (1 / (1 - R12_squared)) # Var(β2)
MSE_diff = (S12 / S11)**2 * (Var_beta2_hat - Beta2_squared) # MSEの差
# 3Dプロットの描画
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dサーフェスプロット
surf = ax.plot_surface(R12_squared, Beta2_squared, MSE_diff, cmap='coolwarm', edgecolor='none')
# 軸ラベルとタイトル
ax.set_title(r'3Dプロット: $\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$ の符号反転', fontsize=14)
ax.set_xlabel(r'$r_{12}^2$ (相関係数の二乗)', fontsize=12)
ax.set_ylabel(r'$\beta_2^2$ (回帰係数の二乗)', fontsize=12)
ax.set_zlabel(r'$\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$', fontsize=12)
# カラーバーの追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=10, label='MSEの差')
plt.tight_layout()
plt.show()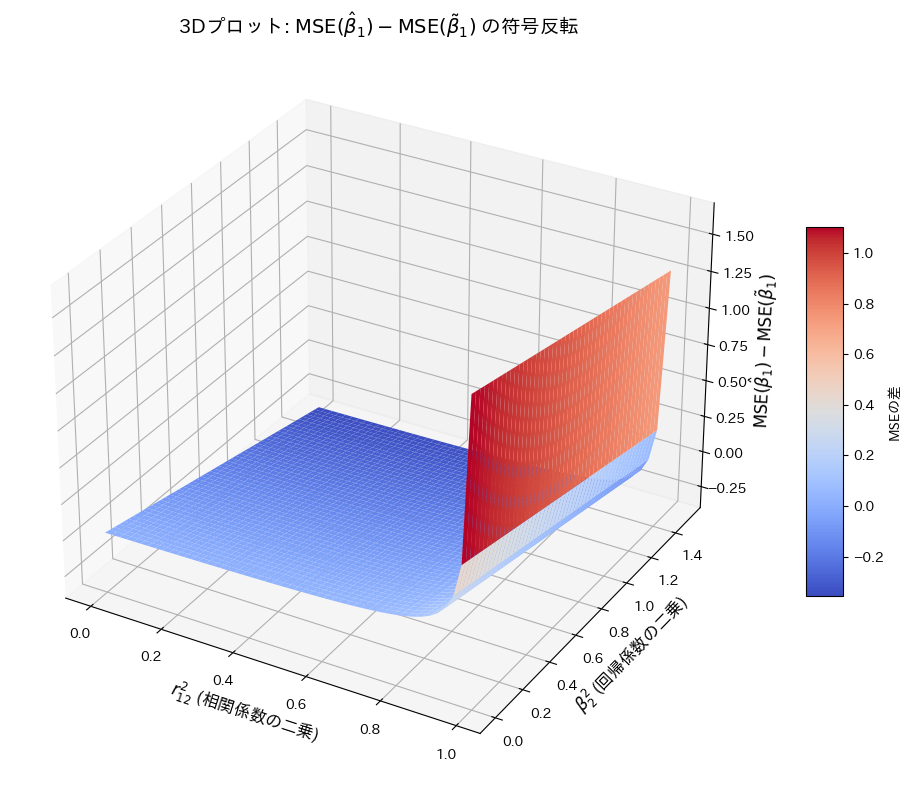
![]() の符号は
の符号は ![]() と
と ![]() の値に依存して変化することが確認できました。
の値に依存して変化することが確認できました。