重回帰モデルの重みの推定量の分散と、説明変数を減らした時のそれとの差を求め、説明変数間の相関係数によるどのような関数になるのか調べました。

コード
![]() の変化が
の変化が![]() と
と![]() に与える影響を、グラフで描画して確認します。
に与える影響を、グラフで描画して確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 2. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_1)$ の比較', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()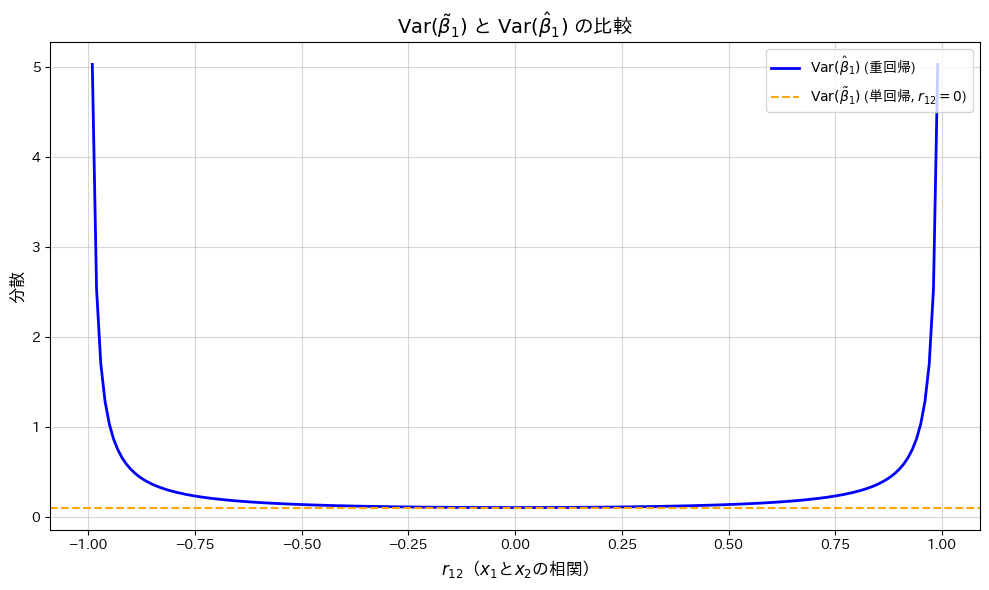
![]() が0に近いほど
が0に近いほど![]() は最小となり、相関が高まると分散が増加する一方で、
は最小となり、相関が高まると分散が増加する一方で、![]() は一定であることが確認されました。
は一定であることが確認されました。
次に、横軸を![]() として、
として、![]() と
と![]() の変化をプロットし、両者の差も併せて確認します。
の変化をプロットし、両者の差も併せて確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# r12^2 の計算
r12_squared_vals = r12_vals**2 # r12^2 の値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_squared_vals)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 分散の差の計算
Var_diff = Var_beta1_hat - Var_beta1_tilde # 分散の差
# グラフのプロット
plt.figure(figsize=(10, 6))
# 分散のプロット
plt.plot(r12_squared_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 分散の差をプロット
plt.plot(r12_squared_vals, Var_diff, label=r'$\mathrm{Var}(\hat{\beta}_1) - \mathrm{Var}(\tilde{\beta}_1)$', color='green', linewidth=2, linestyle=':')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$, $\mathrm{Var}(\hat{\beta}_1)$ とその差の比較 ($r_{12}^2$)', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}^2$(相関係数の二乗)', fontsize=12)
plt.ylabel(r'分散 / 差', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()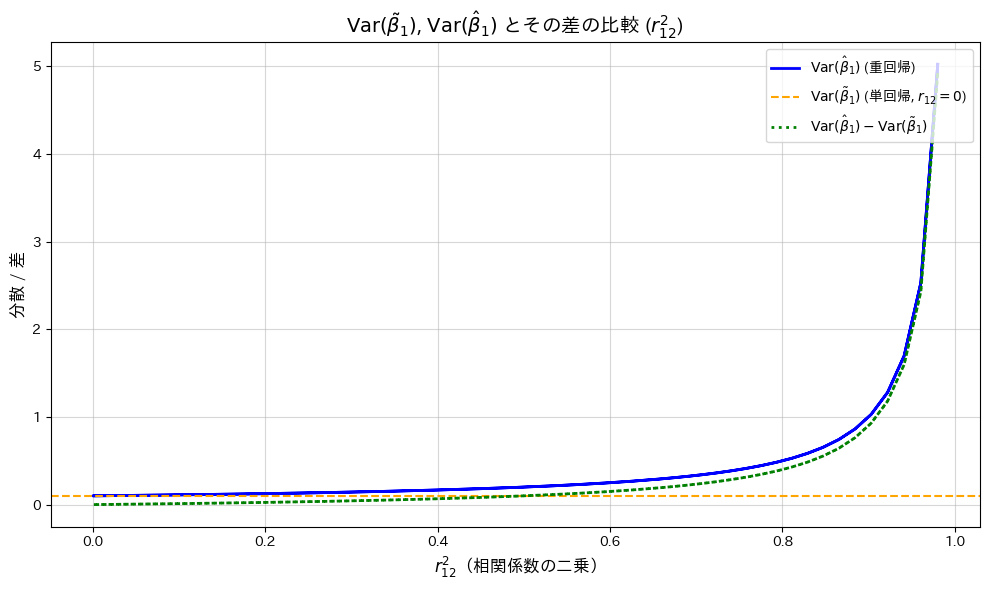
![]() が
が![]() の単調増加関数であることが確認されました。
の単調増加関数であることが確認されました。