前問の検定がネイマン-ピアソンの基本定理に基づき一様最強力検定であることを示しました。

コード
有意水準α=0.05のもと、検出力を理論値とシミュレーションで描画し比較します。
# 2015 Q2(5) 2024.12.11
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーション設定
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
num_simulations = 10000 # シミュレーション回数
n = 10 # 標本サイズ
mu_values = np.linspace(0, 2, 10) # 真の平均 μ の範囲
# 臨界値の計算
critical_value = z_alpha / np.sqrt(n) # 棄却域の閾値
# 検出力を計算する関数
def compute_power_for_mu(mu, n, z_alpha):
return 1 - norm.cdf(z_alpha - mu * np.sqrt(n))
# シミュレーションで検出力を計算
empirical_powers = []
for mu in mu_values:
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations) # 標本生成
rejection_rate = np.mean(samples > critical_value) # 棄却割合
empirical_powers.append(rejection_rate)
# 理論的な検出力を計算
theoretical_powers = [compute_power_for_mu(mu, n, z_alpha) for mu in mu_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, theoretical_powers, label="理論的検出力", linestyle="--", color="blue")
plt.scatter(mu_values, empirical_powers, label="シミュレーションによる検出力", color="red", zorder=5)
plt.axhline(y=0.05, color="green", linestyle="--", label="有意水準 $\\alpha = 0.05$")
# グラフ設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
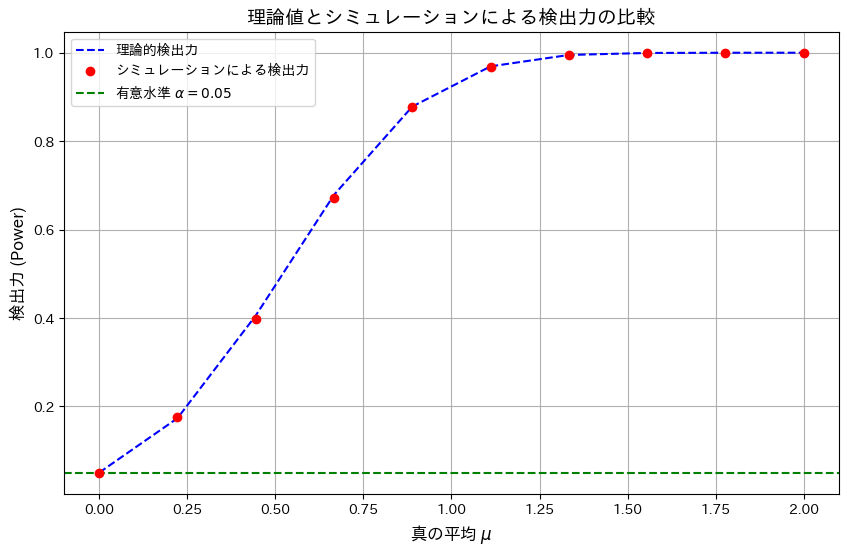
検出力は理論値とシミュレーションでよく一致し、検定が正しく機能していることを確認しました。また、真の平均μ>0に対して検出力が単調増加することが分かり、この検定が一様最強力検定の特徴を備えていることが確認できました。