標本平均の片側検定での検出力を特定の値以上にするために必要なサンプル数を求めました。
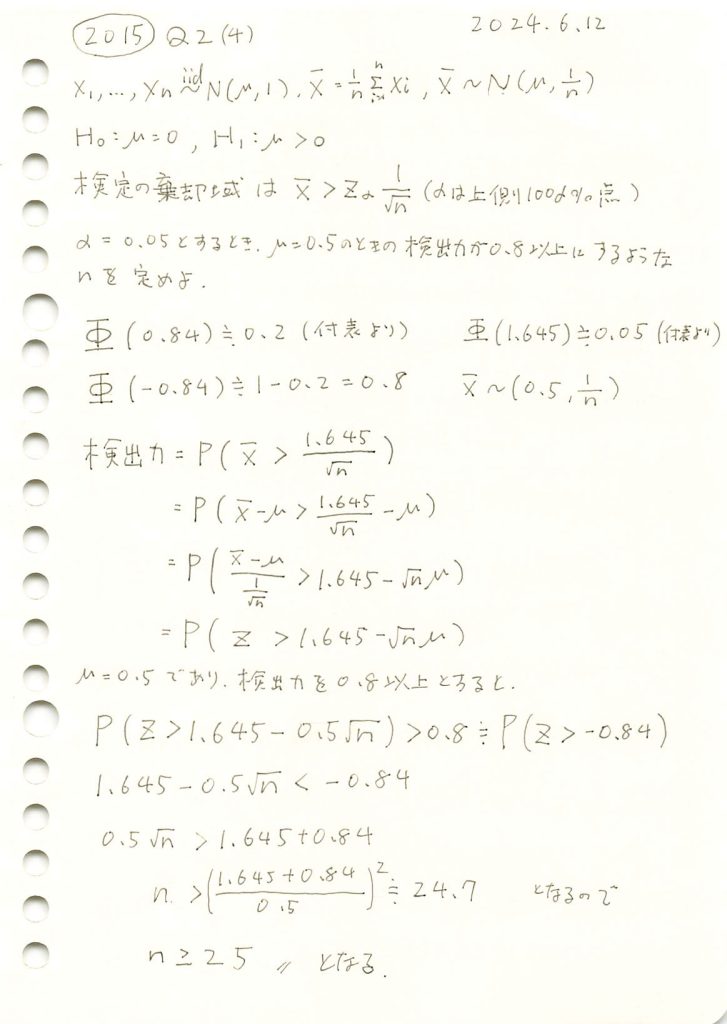
コード
有意水準α=0.05において、標本サイズnと検出力の関係を理論値とシミュレーションで比較し、目標の検出力0.8を達成するために必要な標本サイズnを調べます。
# 2015 Q2(4) 2024.12.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 設定
alpha = 0.05 # 有意水準
target_power = 0.8 # 目標検出力
mu = 0.5 # 真の平均
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
z_power = norm.ppf(target_power) # 検出力に対応する Z 値
# 理論的な検出力の計算
n_values = np.arange(1, 51, 1) # 標本の大きさ n = 1, 2, ..., 50
powers_theoretical = [1 - norm.cdf(z_alpha - mu * np.sqrt(n)) for n in n_values]
# 実際の検出力を乱数シミュレーションで計算
num_simulations = 10000 # シミュレーション回数
n_sim_values = np.arange(5, 51, 5) # n = 5, 10, ..., 50
powers_simulated = []
for n in n_sim_values:
# 標本平均を生成
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations)
# 標本平均が臨界値を超えた割合を計算
rejection_rate = np.mean(samples > z_alpha / np.sqrt(n))
powers_simulated.append(rejection_rate)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的な検出力の曲線
plt.plot(n_values, powers_theoretical, label="理論的な検出力 (Power)", color="blue")
# シミュレーションによる検出力
plt.scatter(n_sim_values, powers_simulated, color="red", label="シミュレーションによる検出力", zorder=5)
# 検出力の目標ラインと必要な標本サイズライン
plt.axhline(y=target_power, color="red", linestyle="--", label=f"目標検出力 Power = {target_power}")
plt.axvline(x=25, color="green", linestyle="--", label="必要な標本数 n = 25")
# グラフの設定
plt.xlabel("標本の大きさ $n$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()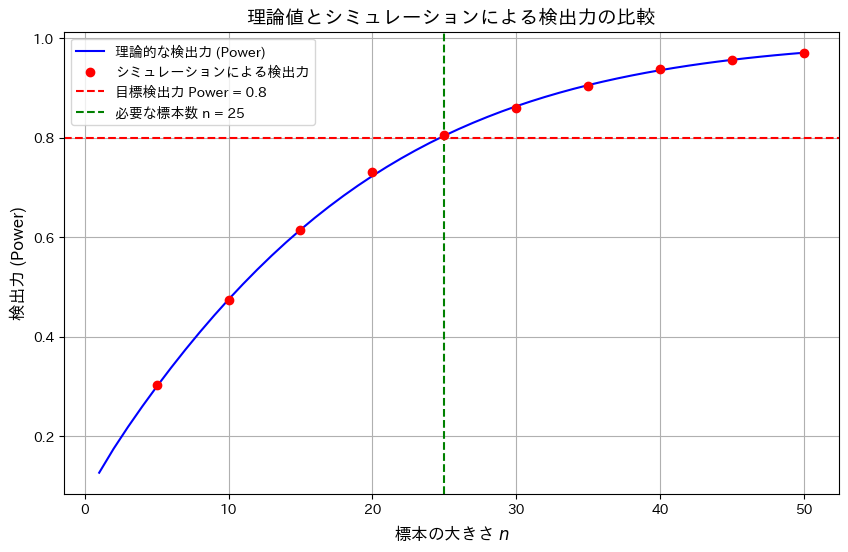
標本サイズnの増加が検出力の向上に寄与することを確認しました。また理論とシミュレーション結果が一致し、目標の検出力0.8を達成するためにはn=25が必要であることが確認できました。