標本平均の片側検定での検出力を求め、母平均と検出力の関係を描きました。

コード
有意水準 α=0.05、サンプルサイズ n=9およびn=16の場合における検出力を真の平均 μを変化させて視覚化します。また、μ=0.4,0.8での検出力を計算します。
# 2015 Q2(3) 2024.12.9
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定義
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
sample_sizes = [9, 16] # n = 9, 16
true_means = [0.4, 0.8] # 真の平均 μ = 0.4, 0.8
# 検出力の計算関数
def compute_power(mu, n, z_alpha):
z_value = z_alpha - mu * np.sqrt(n)
power = 1 - norm.cdf(z_value)
return power
# 検出力を計算
mu_values = np.linspace(0, 1.5, 100) # 真の平均 μ の範囲
powers_n9 = [compute_power(mu, n=9, z_alpha=z_alpha) for mu in mu_values]
powers_n16 = [compute_power(mu, n=16, z_alpha=z_alpha) for mu in mu_values]
# 指定された μ = 0.4, 0.8 の検出力を計算
specific_powers = {
(n, mu): compute_power(mu, n, z_alpha)
for n in sample_sizes
for mu in true_means
}
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, powers_n9, label="検出力 (n=9)", linestyle="--", color="blue")
plt.plot(mu_values, powers_n16, label="検出力 (n=16)", linestyle="-", color="green")
# μ = 0.4, 0.8 の場合の検出力をプロット
for (n, mu), power in specific_powers.items():
plt.scatter(mu, power, label=f"n={n}, μ={mu}, Power={power:.2f}", zorder=5)
# グラフの設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("検出力の挙動 ($n=9$ および $n=16$ の場合)", fontsize=14)
plt.axhline(y=alpha, color="red", linestyle=":", label=f"有意水準 α={alpha}")
plt.legend()
plt.grid(True)
plt.show()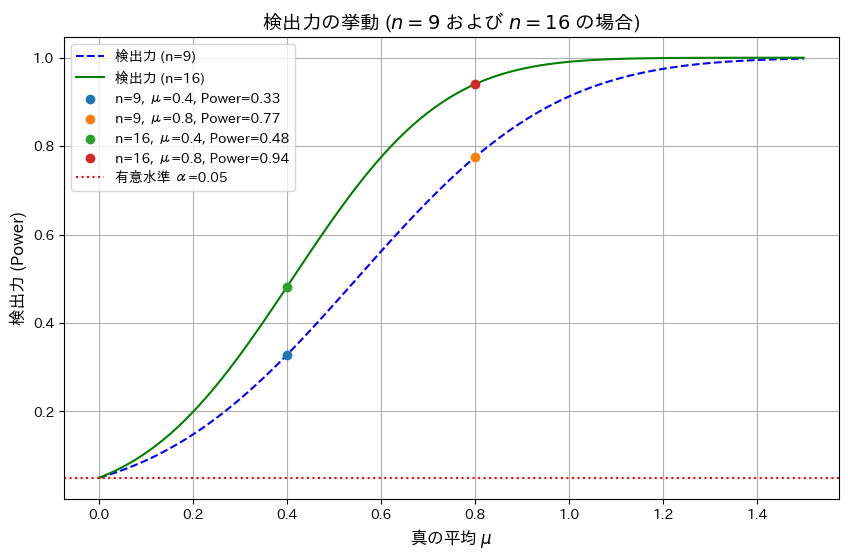
シミュレーションの結果、サンプルサイズnが増加することで検出力が向上することと、真の平均μが大きくなるほど検出力が1に近づくことが分かりました。