不偏分散の定数C倍を母分散の推定量とし平均二乗誤差を最小とするCを求めました。
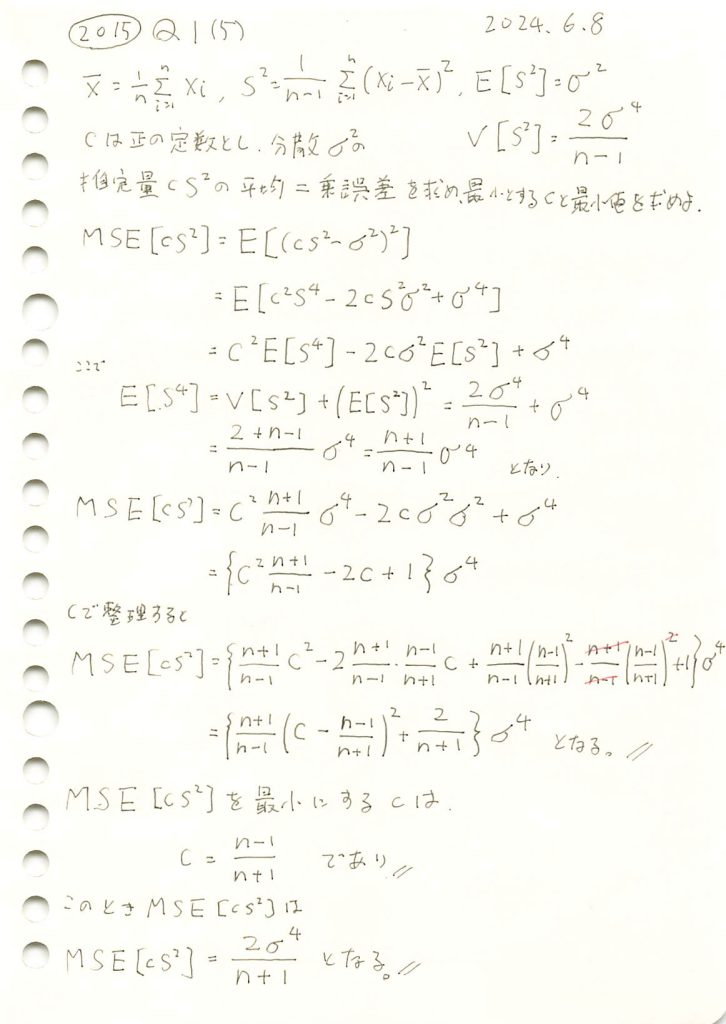
コード
![]() を最小にするcが
を最小にするcが![]() であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
# 2015 Q1(5) 2024.12.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n = 20 # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 理論値計算
c_theoretical = (n - 1) / (n + 1) # 理論的に最適な c
mse_theoretical_min = sigma2**2 * (2 / (n + 1)) # 最小 MSE の理論値
# シミュレーションで MSE を計算
c_values = np.linspace(0.5, 1.5, 100) # c をいろいろ変化させる
mse_simulated = []
for c in c_values:
simulated_errors = []
for _ in range(num_simulations):
sample = np.random.normal(0, sigma, n)
s2 = np.var(sample, ddof=1) # 不偏分散
error = (c * s2 - sigma2) ** 2 # 誤差の二乗
simulated_errors.append(error)
mse_simulated.append(np.mean(simulated_errors))
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(c_values, mse_simulated, label="シミュレーションによる MSE", color='blue')
plt.axvline(c_theoretical, color='orange', linestyle='--', label=f"理論的な c={c_theoretical:.2f}")
plt.axhline(mse_theoretical_min, color='green', linestyle='--', label=f"最小理論 MSE={mse_theoretical_min:.2f}")
plt.title("MSE のシミュレーションと理論値")
plt.xlabel("c の値")
plt.ylabel("MSE")
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()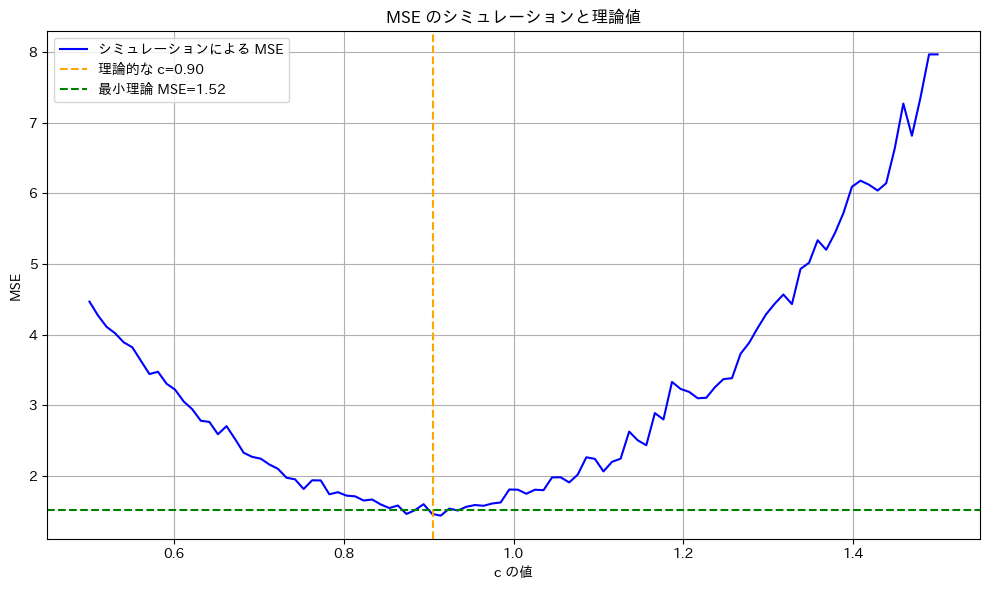
![]() は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。
は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。