不偏分散が母分散の不偏推定量である事を示しました。
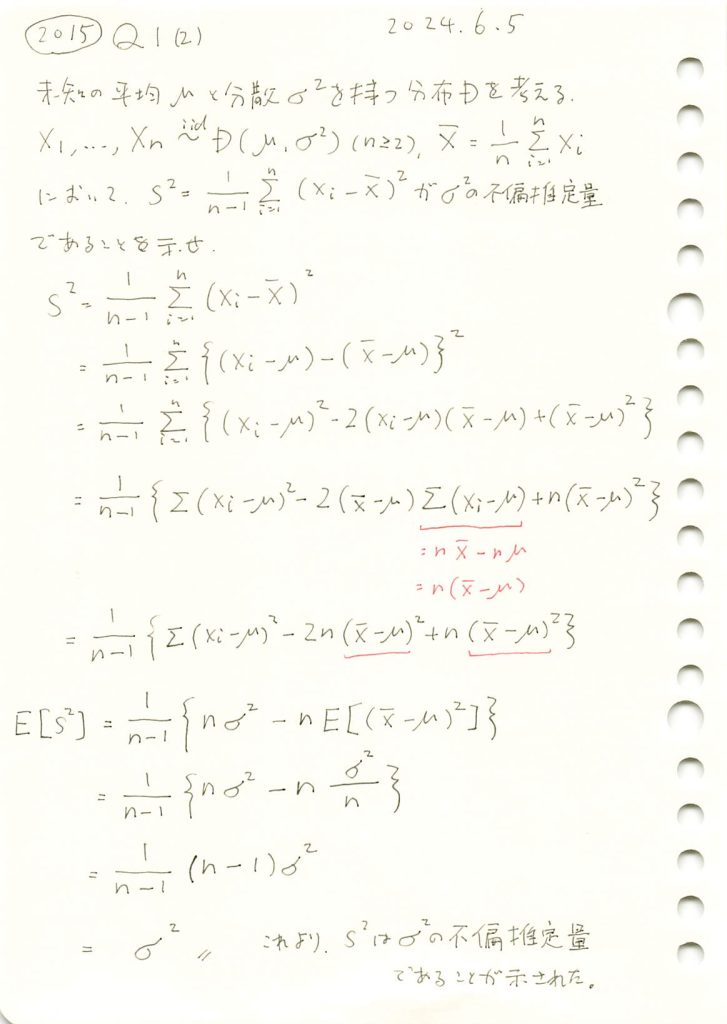
コード
※2018 Q1(1)から引用https://statistics.blue/2018-q11/
nを2~100に変化させて、不偏分散と標本分散を比較してみます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母集団平均
sigma = 2 # 母集団標準偏差
sigma_squared = sigma ** 2 # 真の母分散
n_values = range(2, 101, 2) # サンプルサイズ n を2から100まで2ステップで変化させる
num_trials = 3000 # 各 n に対して100回の試行を行う
# 不偏分散 (1/(n-1)) と 標本分散 (1/n) を計算するためのリスト
unbiased_variances = []
biased_variances = []
# 各サンプルサイズ n で分散を計算
for n in n_values:
unbiased_variance_sum = 0
biased_variance_sum = 0
# 各サンプルサイズ n に対して複数回試行して平均を計算
for _ in range(num_trials):
# 正規分布に従うサンプルを生成
sample = np.random.normal(mu, sigma, n)
# 標本平均
sample_mean = np.mean(sample)
# 不偏分散 (1/(n-1))
unbiased_variance = np.sum((sample - sample_mean) ** 2) / (n - 1)
unbiased_variance_sum += unbiased_variance
# 標本分散 (1/n)
biased_variance = np.sum((sample - sample_mean) ** 2) / n
biased_variance_sum += biased_variance
# 各 n に対する平均分散をリストに追加
unbiased_variances.append(unbiased_variance_sum / num_trials)
biased_variances.append(biased_variance_sum / num_trials)
# グラフを描画
plt.plot(n_values, unbiased_variances, label="不偏分散 (1/(n-1))", color='blue', marker='o')
plt.plot(n_values, biased_variances, label="標本分散 (1/n)", color='red', linestyle='--', marker='x')
# 真の分散を水平線で描画
plt.axhline(y=sigma_squared, color='green', linestyle='-', label=f'真の分散 = {sigma_squared}')
# グラフの設定
plt.title('サンプルサイズに対する標本分散と不偏分散の比較')
plt.xlabel('サンプルサイズ n')
plt.ylabel('分散')
plt.legend()
plt.grid(True)
plt.show()
標本分散には不偏性はなく、不偏分散には不偏性があることが確認できました。
次に、![]() と
と![]() を棒グラフで比較してみます。
を棒グラフで比較してみます。
# 2015 Q1(2) 2024.12.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母平均
sigma = 2 # 母標準偏差
n = 10 # 標本サイズ
num_simulations = 30 # シミュレーション回数
# 共通のシミュレーションサンプルを生成
samples = [np.random.normal(mu, sigma, n) for _ in range(num_simulations)]
# 各シミュレーションで E[(X - X̄)^2] と E[(X - μ)^2] を計算
var_sample_mean = [np.mean((sample - np.mean(sample))**2) for sample in samples] # E[(X - X̄)^2]
var_population_mean = [np.mean((sample - mu)**2) for sample in samples] # E[(X - μ)^2]
# 棒グラフの準備
x = np.arange(1, num_simulations + 1) # シミュレーション番号
plt.figure(figsize=(12, 6))
# 棒グラフをプロット
plt.bar(x - 0.2, var_sample_mean, width=0.4, label=r"$E[(X - \overline{X})^2]$", color='blue', alpha=0.7)
plt.bar(x + 0.2, var_population_mean, width=0.4, label=r"$E[(X - \mu)^2]$", color='orange', alpha=0.7)
# グラフ
plt.title(r"$E[(X - \overline{X})^2]$ と $E[(X - \mu)^2]$ の比較")
plt.xlabel("シミュレーション番号")
plt.ylabel("値")
plt.xticks(x) # シミュレーション番号をx軸に設定
plt.legend()
plt.grid(axis='y')
# 表示
plt.tight_layout()
plt.show()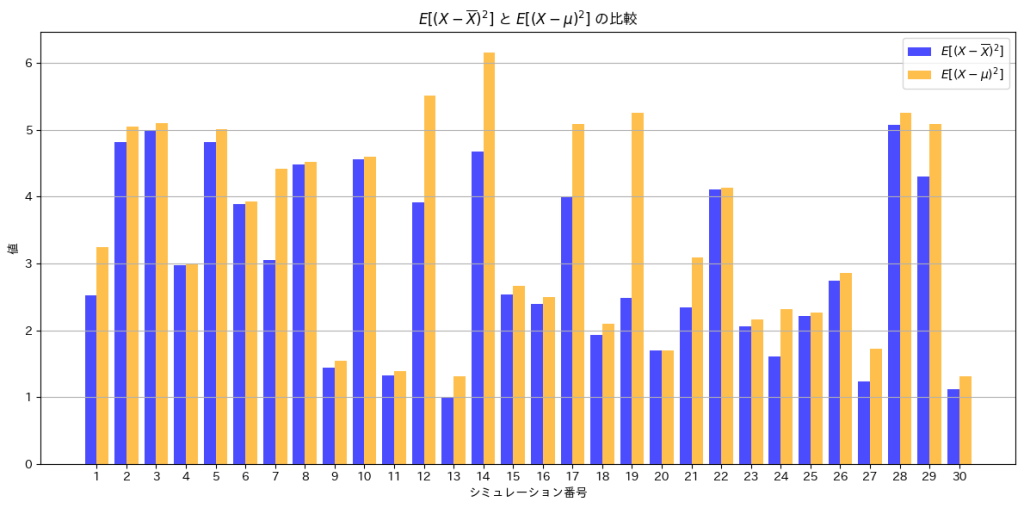
![]() は、
は、![]() よりも小さくなっていることが分かります。不偏分散
よりも小さくなっていることが分かります。不偏分散![]() は、nでなくn-1で割ることで、母分散の推定値として偏りを修正しています。
は、nでなくn-1で割ることで、母分散の推定値として偏りを修正しています。