任意の分布に従う確率変数の平均の二乗の期待値を求めました。
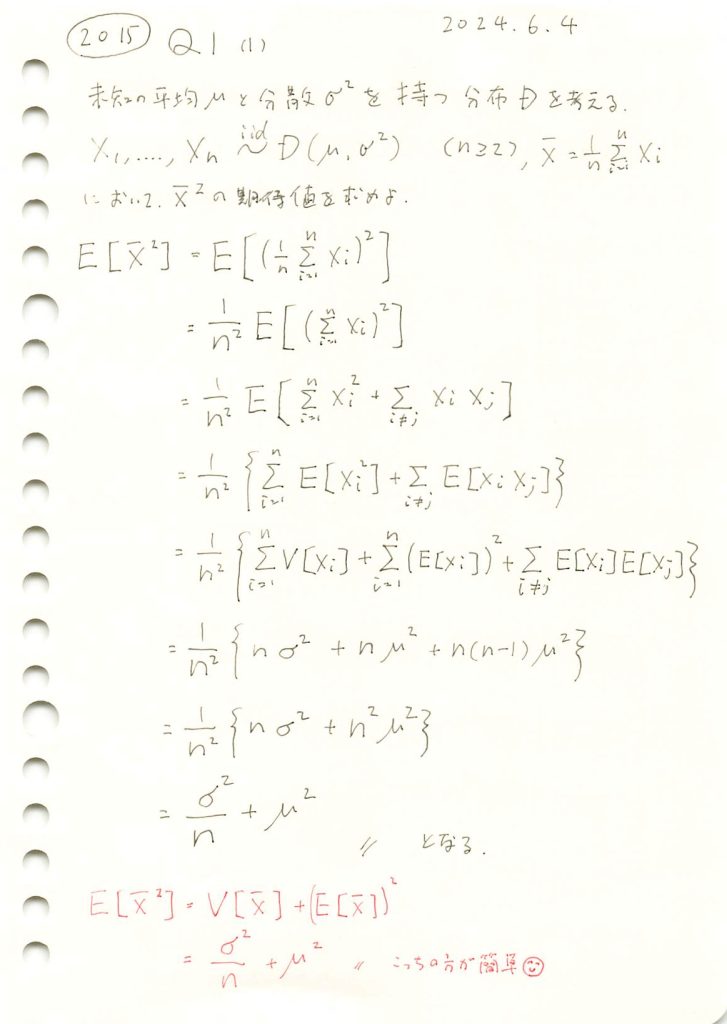
コード
![]() を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した
を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した![]() を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
#2015 Q1(1) 2024.12.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ncx2
# パラメータ設定(nを複数用意)
n_values = [5, 10, 20, 50] # 標本サイズのリスト
mu = 4 # 母平均
sigma2 = 5 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
num_simulations = 10000 # シミュレーション回数
# 暖色系カラーパレットの設定
colors = plt.cm.autumn(np.linspace(0, 1, len(n_values)))
# 描画の準備
plt.figure(figsize=(10, 8))
# 結果格納用
results = []
# nごとに分布をシミュレーションし、プロット
for i, n in enumerate(n_values):
# シミュレーションによる標本平均の二乗 (X̄^2) の生成
sample_means_squared = np.array([
np.mean(np.random.normal(mu, sigma, n))**2 for _ in range(num_simulations)
])
# シミュレーションによる期待値 E[X̄^2] の計算
simulated_mean = np.mean(sample_means_squared)
# 理論値の計算
theoretical_mean = sigma2 / n + mu**2
# 結果を記録
results.append((n, theoretical_mean, simulated_mean))
# ヒストグラムをプロット
plt.hist(
sample_means_squared, bins=30, density=True, alpha=0.5,
label=f"n={n}, 理論値: {theoretical_mean:.3f}, シミュレーション値: {simulated_mean:.3f}",
color=colors[i]
)
# 非心カイ二乗分布のPDFをプロット
x_values = np.linspace(0, np.max(sample_means_squared), 1000)
df = 1 # 自由度は標本平均の二乗の場合、1となる
nc = (n * mu**2) / sigma2 # 非心度 λ
theoretical_pdf = ncx2.pdf(x_values, df, nc, scale=sigma2 / n)
plt.plot(
x_values, theoretical_pdf, linewidth=2, label=f"n={n} の非心カイ二乗分布", color=colors[i]
)
# グラフ
plt.title("標本平均の二乗 ($\\overline{X}^2$) の分布と非心カイ二乗分布")
plt.xlabel("$\\overline{X}^2$")
plt.ylabel("密度")
plt.legend()
plt.grid()
plt.show()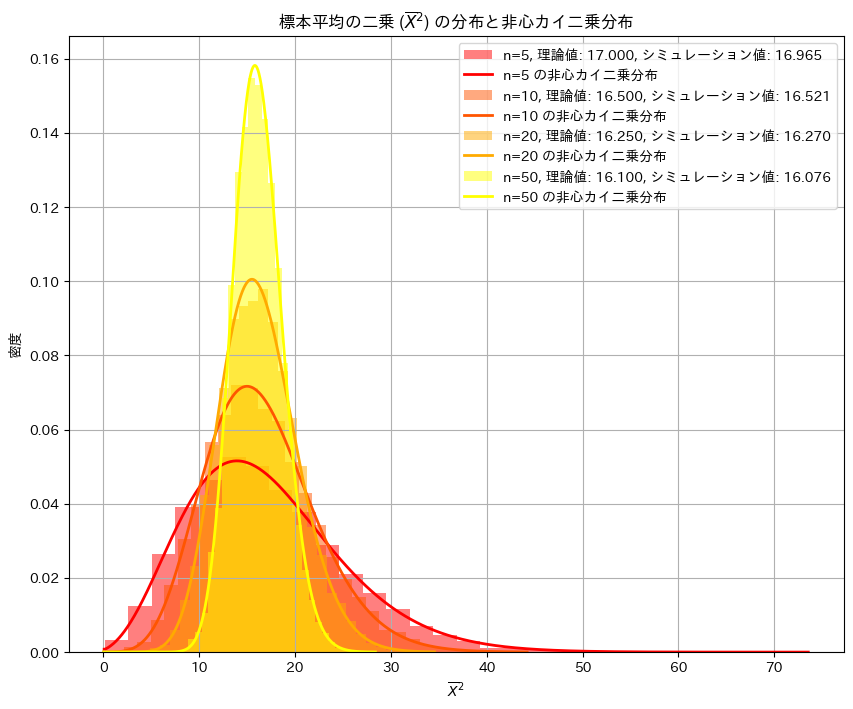
シミュレーションの結果、![]() と
と![]() は概ね一致しました。また
は概ね一致しました。また![]() の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。
の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。