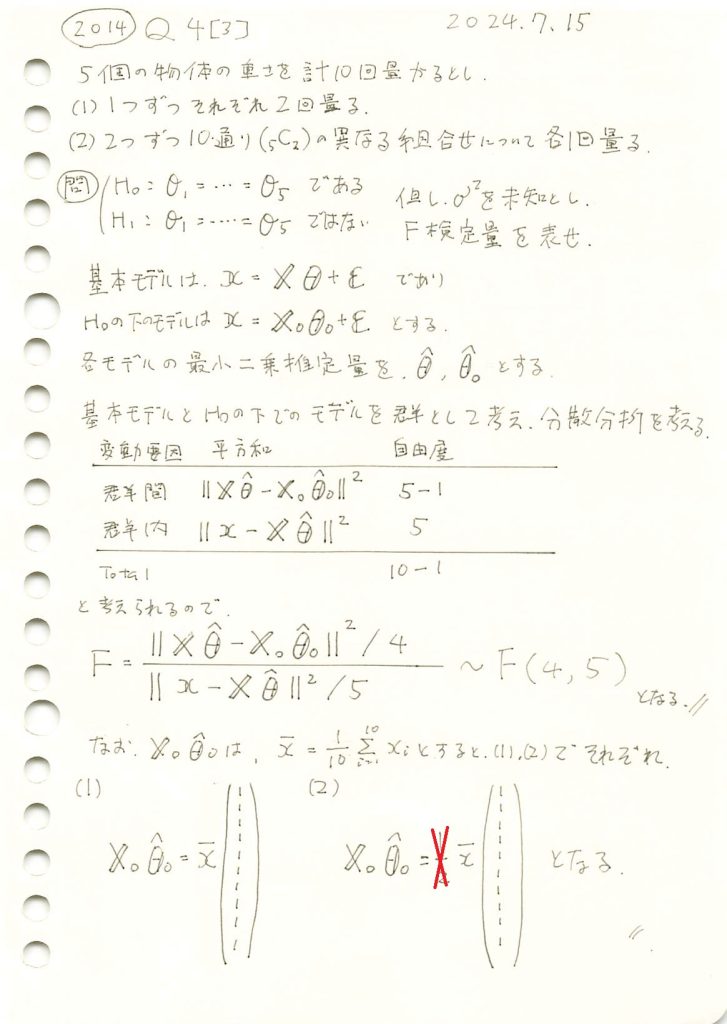
5個の物体の重さを、1つずつ2回量る場合と、2つずつ10通り量る場合で、誤差の分散を未知とし、全ての物体の重さが等しいとする帰無仮説を検定するF検定量を求めました。
コード
真の値![]() とし、二つの測定方法(1)と(2)においてシミュレーションを行い、F統計量を計算して、帰無仮説H0が棄却されるかを検定を行います。
とし、二つの測定方法(1)と(2)においてシミュレーションを行い、F統計量を計算して、帰無仮説H0が棄却されるかを検定を行います。
# 2014 Q4(3) 2025.1.11
import numpy as np
from scipy.stats import f
# パラメータ設定
n = 10 # 観測データ数
p_1 = 5 # 自由度(対立仮説モデルのパラメータ数)
p_0 = 1 # 自由度(帰無仮説モデルのパラメータ数)
nu_1 = p_1 - p_0 # 分子の自由度
nu_2 = n - p_1 # 分母の自由度
# 設計行列
X1 = np.array([ # 測定法 (1)
[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 1]
])
X2 = np.array([ # 測定法 (2)
[1, 1, 0, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 0, 1, 0],
[1, 0, 0, 0, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1],
[0, 0, 1, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 1, 1]
])
X0 = np.ones((n, 1)) # 帰無仮説モデルの設計行列
# シミュレーション設定
true_theta = np.array([10, 10, 10, 10, 10]) # 真の値 (帰無仮説下)
sigma_squared = 1 # 誤差分散
n_simulations = 10000 # シミュレーション回数
# 統計量を保存するリスト
f_statistics_1 = []
f_statistics_2 = []
# シミュレーション
for _ in range(n_simulations):
# 観測データ生成
epsilon = np.random.normal(0, np.sqrt(sigma_squared), n)
x1 = X1 @ true_theta + epsilon
x2 = X2 @ true_theta + epsilon
# 最小二乗推定量
theta_hat_1 = np.linalg.inv(X1.T @ X1) @ X1.T @ x1
theta_hat_2 = np.linalg.inv(X2.T @ X2) @ X2.T @ x2
theta_hat_0_1 = np.linalg.inv(X0.T @ X0) @ X0.T @ x1
theta_hat_0_2 = np.linalg.inv(X0.T @ X0) @ X0.T @ x2
# 分子と分母の計算
numerator_1 = np.sum((X1 @ theta_hat_1 - X0 @ theta_hat_0_1) ** 2) / nu_1
denominator_1 = np.sum((x1 - X1 @ theta_hat_1) ** 2) / nu_2
f_stat_1 = numerator_1 / denominator_1
numerator_2 = np.sum((X2 @ theta_hat_2 - X0 @ theta_hat_0_2) ** 2) / nu_1
denominator_2 = np.sum((x2 - X2 @ theta_hat_2) ** 2) / nu_2
f_stat_2 = numerator_2 / denominator_2
f_statistics_1.append(f_stat_1)
f_statistics_2.append(f_stat_2)
# 平均 F 統計量を計算
f_stat_mean_1 = np.mean(f_statistics_1)
f_stat_mean_2 = np.mean(f_statistics_2)
# 理論 F 分布の平均計算
f_theoretical_mean = nu_2 / (nu_2 - 2) if nu_2 > 2 else None
# P値の計算
p_value_1 = 1 - f.cdf(f_stat_mean_1, nu_1, nu_2)
p_value_2 = 1 - f.cdf(f_stat_mean_2, nu_1, nu_2)
# 有意水準
alpha = 0.05
reject_null_1 = p_value_1 < alpha
reject_null_2 = p_value_2 < alpha
# 結果を出力
print("理論 F 分布の平均 (自由度 ν1 = {0}, ν2 = {1}): {2:.4f}".format(nu_1, nu_2, f_theoretical_mean))
print("\n測定法 (1):")
print(" 平均 F 統計量: {:.4f}".format(f_stat_mean_1))
print(" P値: {:.4e}".format(p_value_1))
print(" 帰無仮説を棄却するか: {}".format("はい" if reject_null_1 else "いいえ"))
print("\n測定法 (2):")
print(" 平均 F 統計量: {:.4f}".format(f_stat_mean_2))
print(" P値: {:.4e}".format(p_value_2))
print(" 帰無仮説を棄却するか: {}".format("はい" if reject_null_2 else "いいえ"))理論 F 分布の平均 (自由度 ν1 = 4, ν2 = 5): 1.6667
測定法 (1):
平均 F 統計量: 1.6255
P値: 3.0067e-01
帰無仮説を棄却するか: いいえ
測定法 (2):
平均 F 統計量: 1.6490
P値: 2.9569e-01
帰無仮説を棄却するか: いいえ二つの測定方法(1)と(2)においてシミュレーションを行い、F検定の結果、どちらの場合も帰無仮説H0が棄却されませんでした。