液体のサンプルの体積と重さから得た比重βがβ0であるという帰無仮説が棄却されないβの信頼区間を体積と重さの分散が既知の場合で求めました。

コード
分散既知の場合の信頼区間をシミュレーションし、カバー率が理論値(1 – α = 0.95)に一致するかを検証してみます。
# 2014 Q3(2) 2025.1.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
n = 30 # サンプルサイズ
beta_true = 1.5 # 真のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均
alpha = 0.05 # 有意水準
num_simulations = 100 # シミュレーション回数
# 分散既知の場合の信頼区間計算関数
def precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha):
X_bar = np.mean(X)
Y_bar = np.mean(Y)
z_alpha = norm.ppf(1 - alpha / 2)
numerator = n * X_bar * Y_bar
term1 = (n * X_bar * Y_bar)**2
term2 = (n * X_bar**2 - z_alpha**2 * sigma_X**2)
term3 = (n * Y_bar**2 - z_alpha**2 * sigma_Y**2)
denominator = n * X_bar**2 - z_alpha**2 * sigma_X**2
if term2 * term3 < 0:
raise ValueError("平方根の中身が負の値です:term2 * term3 は 0 以上でなければなりません。")
sqrt_term = np.sqrt(term1 - term2 * term3)
lower_bound = (numerator - sqrt_term) / denominator
upper_bound = (numerator + sqrt_term) / denominator
return lower_bound, upper_bound
# シミュレーション
intervals_precise = []
contains_true_beta_precise = []
for _ in range(num_simulations):
X = np.random.normal(mu_X, sigma_X, n)
epsilon = np.random.normal(0, np.sqrt(sigma_Y**2 + (beta_true * sigma_X)**2), n)
Y = beta_true * X + epsilon
# 信頼区間を計算
ci = precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha)
intervals_precise.append(ci)
contains_true_beta_precise.append(ci[0] <= beta_true <= ci[1])
# カバー率を計算
cover_rate_precise = sum(contains_true_beta_precise) / num_simulations
print("カバー率:")
print(f" 分散既知の場合: {cover_rate_precise:.4f}")
# 可視化
plt.figure(figsize=(12, 8))
for i, ci in enumerate(intervals_precise):
color = 'green' if contains_true_beta_precise[i] else 'red'
plt.plot([ci[0], ci[1]], [i, i], color=color, marker='o', label="" if i > 0 else "信頼区間")
plt.axvline(x=beta_true, color='blue', linestyle='--', label=f"真のβ: {beta_true}")
plt.title("分散既知の場合の信頼区間 (各シミュレーション)", fontsize=16)
plt.xlabel("β", fontsize=12)
plt.ylabel("シミュレーション回数", fontsize=12)
plt.legend()
plt.grid()
plt.show()カバー率:
分散既知の場合: 0.9500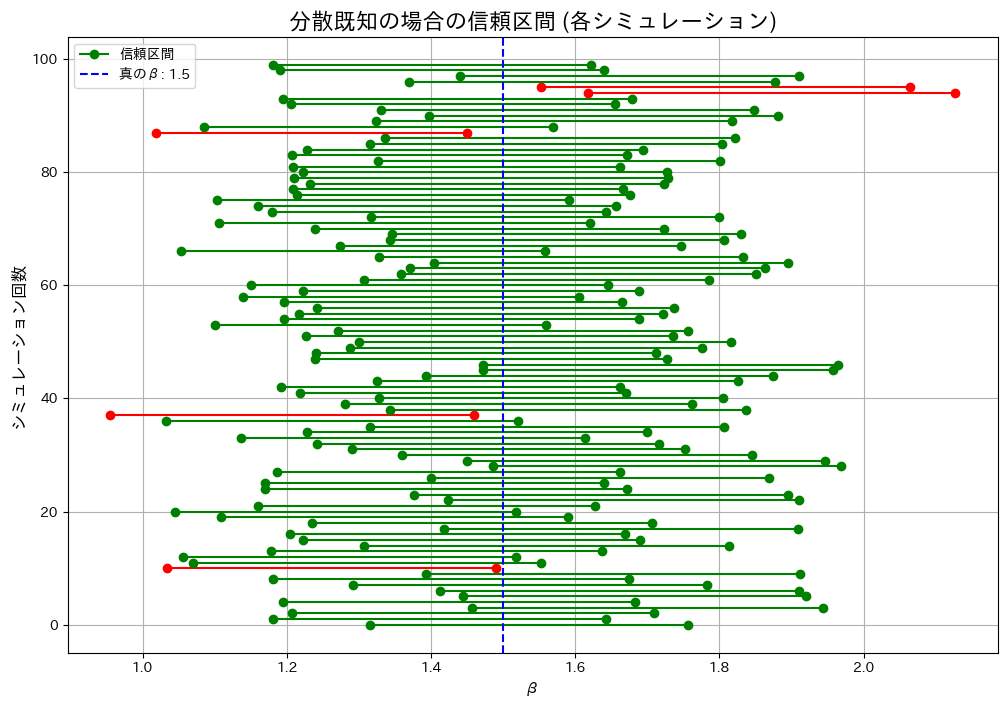
実行ごとに値は変動しましたが、カバー率は概ね理論値(1 – α = 0.95)に一致しました。