n個の一様分布の順序統計量の同時分布が、前問の分布に等しい事を示しました。

コード
![]() と
と![]() の個別の分布をシミュレーションし、グラフを描画してみます。
の個別の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 個別の分布を比較
plt.figure(figsize=(12, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, alpha=0.5, density=True, label=rf"$Y_{i+1}$", histtype='step', linewidth=2)
plt.hist(U[:, i], bins=50, alpha=0.5, density=True, label=rf"$U_{{({i+1})}}$", histtype='step', linestyle='--', linewidth=2)
# グラフの装飾
plt.title("累積比率と順序統計量の個別分布の比較", fontsize=16)
plt.xlabel("値", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()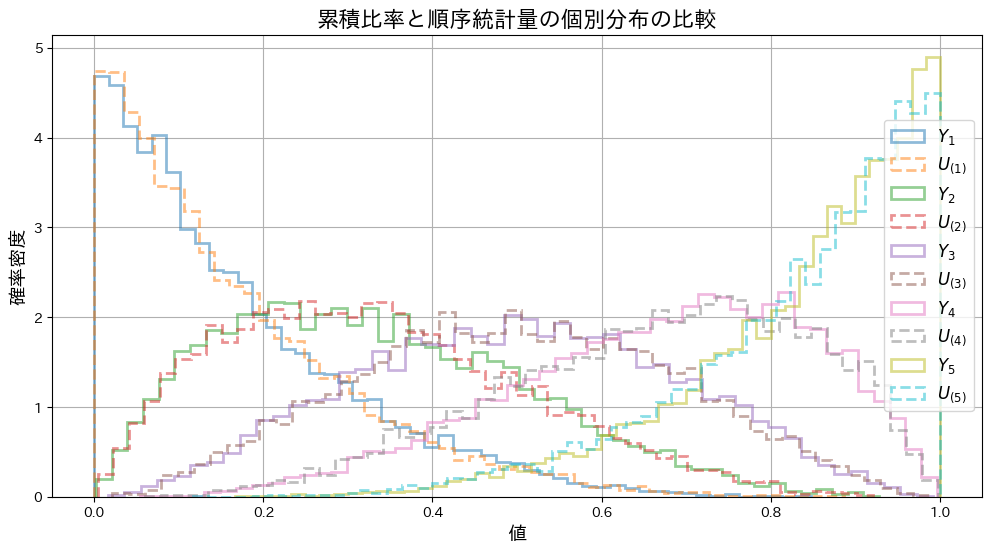
![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
次に、同時確率![]() と
と![]() の分布をシミュレーションし、グラフを描画してみます。
の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 同時確率密度を計算
cumulative_density = np.prod(Y, axis=1) # 累積比率 (Y_1 * Y_2 * ... * Y_n)
order_stats_density = np.prod(U, axis=1) # 順序統計量 (U_(1) * U_(2) * ... * U_(n))
# (5) ヒストグラムを描画して比較
plt.figure(figsize=(12, 6))
# 累積比率分布の同時確率密度
plt.hist(cumulative_density, bins=50, alpha=0.5, density=True, label=r"$f_Y(Y_1, Y_2, \ldots, Y_n)$")
# 順序統計量の同時確率密度
plt.hist(order_stats_density, bins=50, alpha=0.5, density=True, label=r"$f_U(U_{(1)}, U_{(2)}, \ldots, U_{(n)})$")
# グラフの装飾
plt.title("累積比率分布と順序統計量の同時確率密度の比較", fontsize=16)
plt.xlabel("同時確率密度", fontsize=14)
plt.ylabel("頻度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()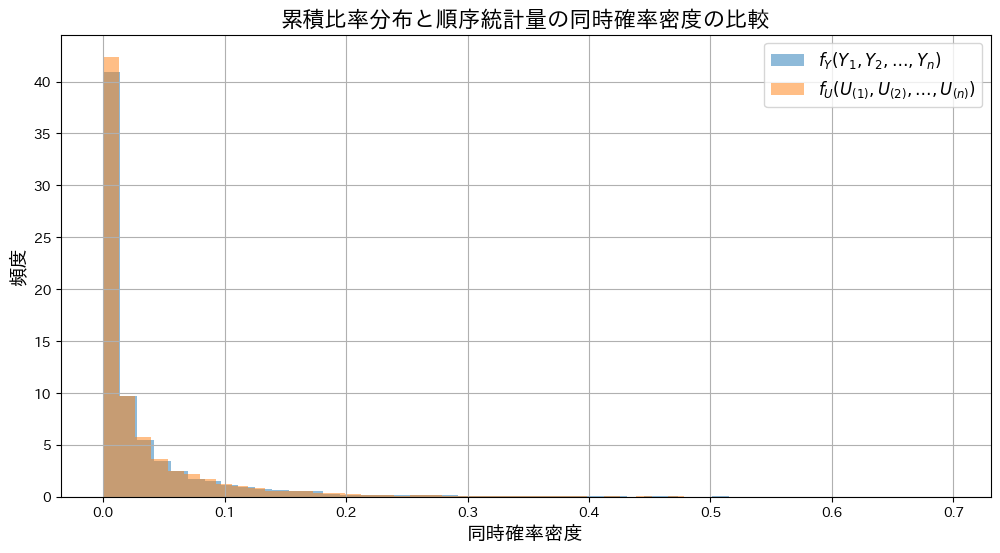
同時確率![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。