形状パラメータが1のガンマ分布は指数分布となり、その和はガンマ分布に従うことを示しました。

コード
TとYの分布についてシミュレーションを行い、それらの形状を視覚化して確認します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
# 修正: Y を累積比率で計算
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # X_1, X_1 + X_2, ..., X_1 + ... + X_n
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# T のヒストグラムを描画
plt.figure(figsize=(10, 6))
t_values = np.linspace(0, 30, 1000)
plt.hist(T, bins=50, density=True, alpha=0.6, color="blue", label="シミュレーション (T)")
plt.plot(t_values, gamma.pdf(t_values, a=n+1, scale=1), color="red", label=f"理論分布 (Gamma({n+1}, 1))")
plt.title("$T$ の分布", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()
# Y の確認 (サンプルの分布)
plt.figure(figsize=(10, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, density=True, alpha=0.5, label=f"$Y_{i+1}$")
plt.title("$Y$ の分布 (各比率)", fontsize=16)
plt.xlabel("$Y_i$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()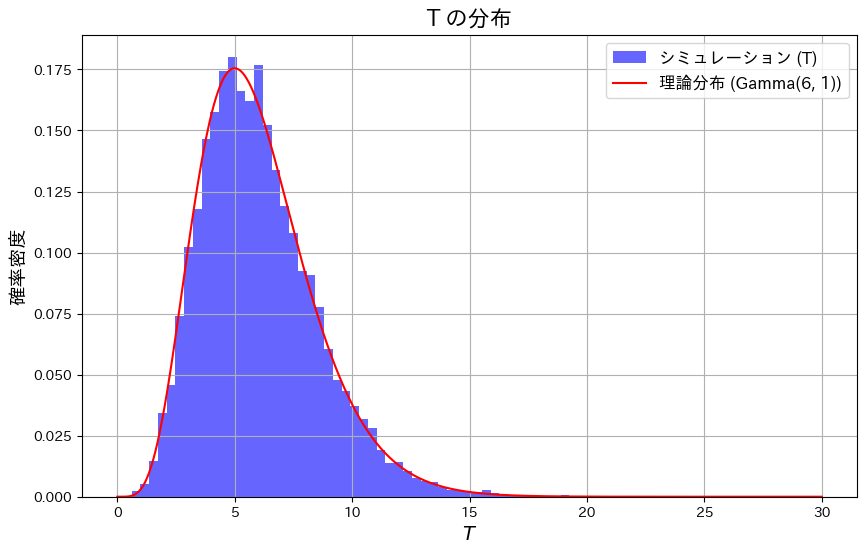
TがGa(n+1,1)のガンマ分布と一致することを確認しました。
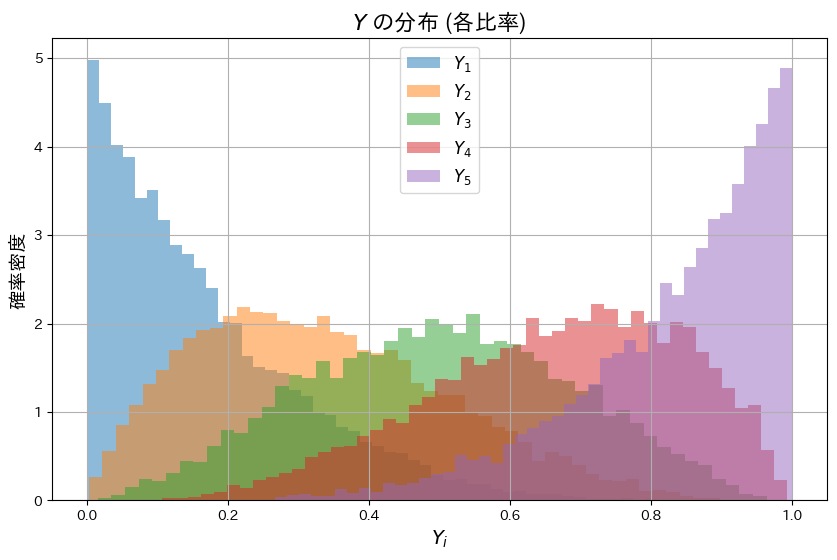
各Yiは累積比率として定義されているため、順序性(Y1<Y2<..<Yn)を持つように見えます。
次に、YiとTが独立であることを確認するため、散布図を描画し、それぞれの共分散Cov(Yi, T)を算出します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
Y = X[:, :-1] / T[:, None] # Y_i = X_i / T (最後の列を除いて正規化)
# (1) 共分散の計算
print("各 Y_i と T の共分散:")
for i in range(n):
cov = np.cov(Y[:, i], T)[0, 1] # 共分散行列から共分散を取得
print(f"Cov(Y_{i+1}, T) = {cov:.5f}")
# (2) 散布図の描画
plt.figure(figsize=(12, 8))
for i in range(n):
plt.scatter(T, Y[:, i], alpha=0.3, label=f"$Y_{i+1}$ vs $T$")
plt.title("散布図: 各 $Y_i$ と $T$ の関係", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("$Y_i$", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()各 Y_i と T の共分散:
Cov(Y_1, T) = 0.00426
Cov(Y_2, T) = 0.00394
Cov(Y_3, T) = -0.00261
Cov(Y_4, T) = -0.00364
Cov(Y_5, T) = -0.00399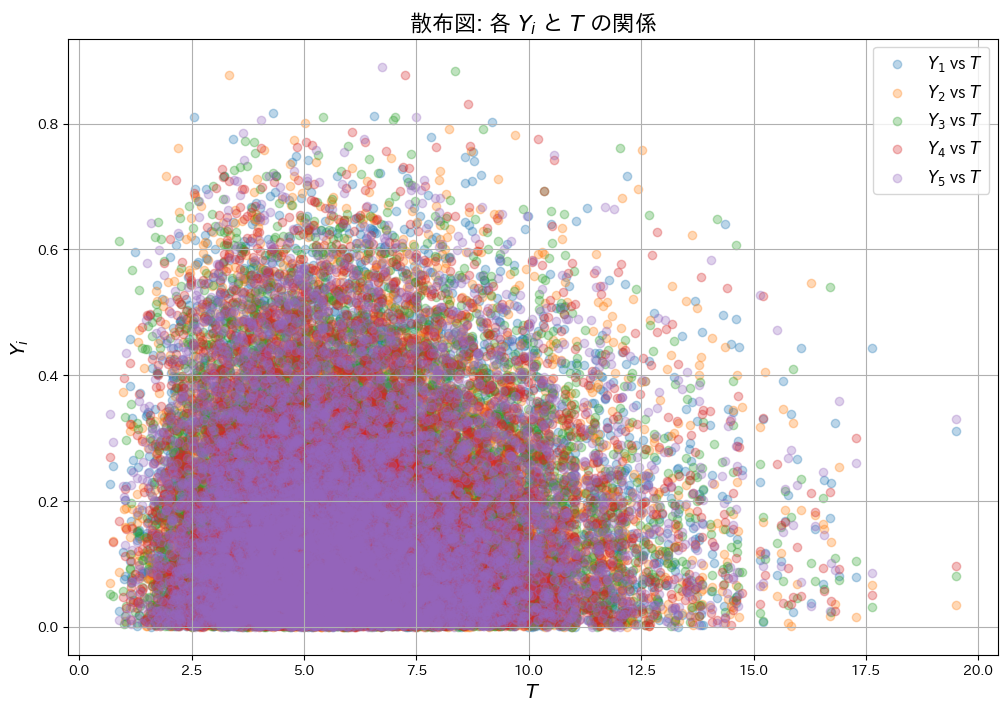
それぞれの共分散Cov(Yi, T)はほぼ0を示し、散布図からもYiとTが互いに影響を与えていないことが確認できました。