二項分布
- 抽出方法: 復元抽出
- 試行の独立性: 各試行は独立
- 確率: 各試行で成功確率は一定
超幾何分布
- 抽出方法: 非復元抽出
- 試行の独立性: 各試行は独立していない
- 確率: 各試行で成功確率が変化
グラフの比較
今回の実験では、二項分布と超幾何分布の違いを視覚的に比較します。二項分布は、復元抽出を行う場合に適用され、各試行が独立しており、成功確率が一定です。一方、超幾何分布は、非復元抽出を行う場合に適用され、試行ごとに成功確率が変化します。実験では、母集団のサイズ、成功対象の数、抽出回数を変え、それぞれのグラフを描画します。特に、サンプルサイズが大きい場合や母集団が小さい場合など、分布の形状に顕著な違いが現れる条件に注目して比較を行います。これにより、抽出方法による分布の違いを視覚的に確認し、二項分布と超幾何分布の特性を理解します。
復元抽出と非復元抽出の比較(広範囲のパラメータ設定)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# パラメータ比を一定に保ったグラフを作成
M_values = [50, 150, 250, 350, 450]
N_A_values = [15, 45, 75, 105, 135] # M の 30%
n_values = [7, 22, 37, 52, 67] # M の 15%
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(5, 1, figsize=(10, 30))
# 異なるパラメータ設定でグラフを描画
for i in range(5):
plot_comparison(M=M_values[i], N_A=N_A_values[i], n=n_values[i], ax=axs[i])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()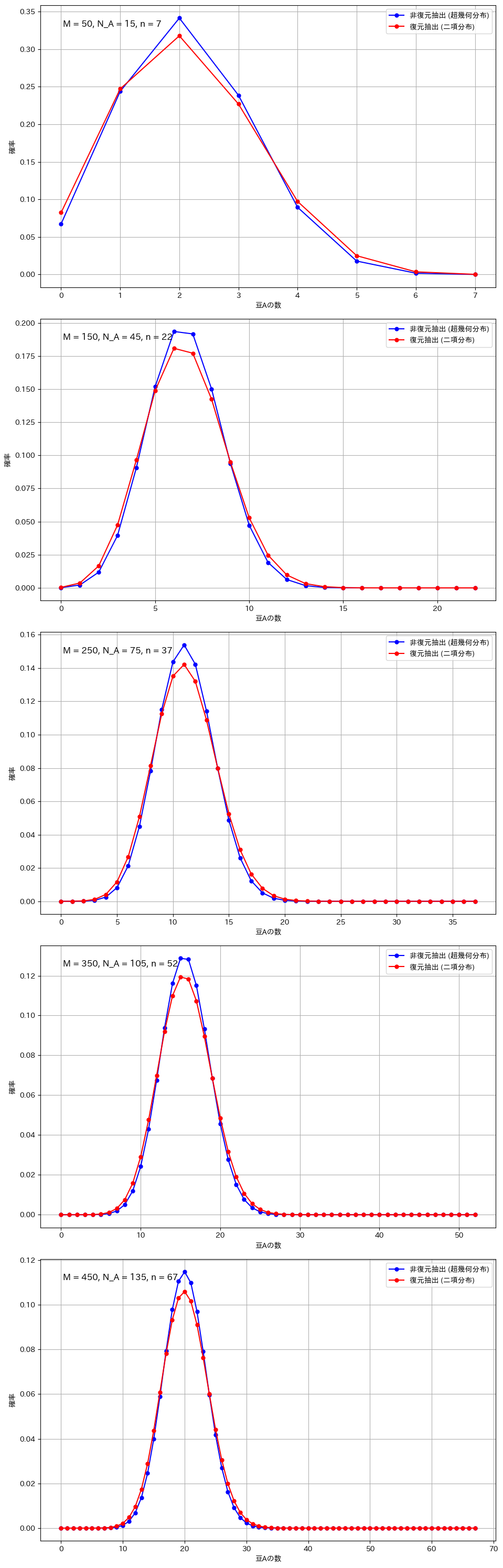
復元抽出と非復元抽出の比較(顕著な違いが現れる条件)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(3, 1, figsize=(10, 18)) # 高さを調整
# 条件1: サンプルサイズが大きい場合
plot_comparison(M=100, N_A=30, n=80, ax=axs[0])
# 条件2: 全体のサイズが小さい場合
plot_comparison(M=20, N_A=6, n=15, ax=axs[1])
# 条件3: 極端な割合の場合
plot_comparison(M=100, N_A=90, n=30, ax=axs[2])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()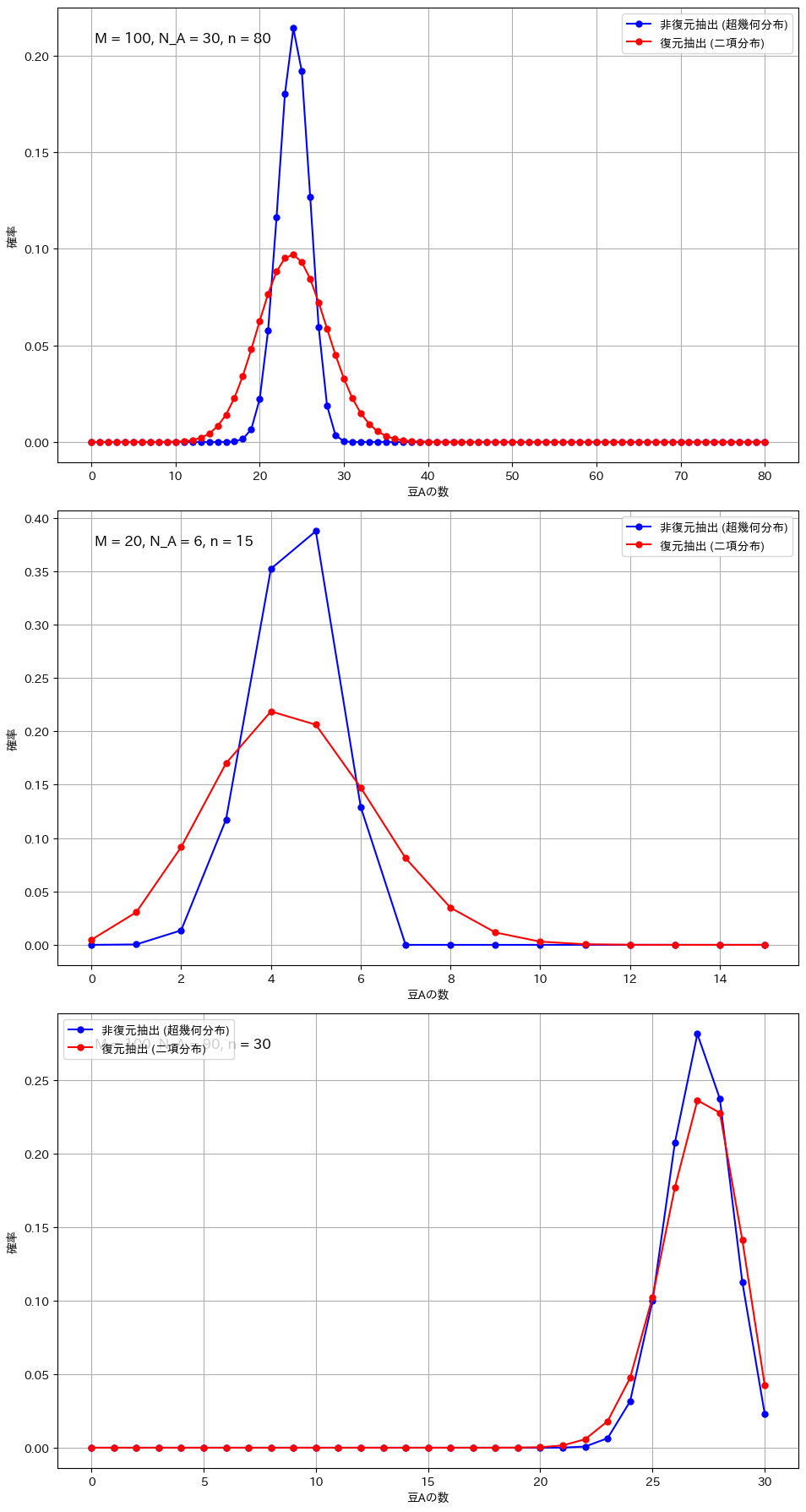
考察
二項分布と超幾何分布の違いが顕著になるのは、サンプルサイズが全体に対して大きい場合や、母集団が小さい場合です。例えば、全体の豆の数が100個で80個を抽出する場合や、母集団が20個でそのうち15個を抽出する場合、非復元抽出では次の試行に与える影響が大きくなり、復元抽出との差が明確に現れます。また、成功確率が極端に高いか低い場合も、非復元抽出の影響で分布が変わりやすくなります。一方、サンプルサイズが小さい場合や母集団が非常に大きい場合には、各抽出の影響が少なく、二項分布と超幾何分布の違いは目立たなくなります。